题目内容
【题目】如图，△ABC中，AB=AC, ∠C=30°，AB的垂直平分线交BC于E,则下列结论正确的是（ ）
A. BE=
CE B. BE=
CE C. BE= 
CE D. 不能确定
【答案】A
【解析】
连接AE，根据垂直平分线的性质得到AE=BE，则∠B=∠BAE=30°，进而得到△ACE为直角三角形，然后根据30°所对应的直角边等于斜边的一半即可得到答案.
解：如图连接AE，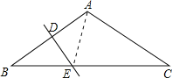
∵△ABC中，AB=AC，∠C=30°，
∴∠B=∠C=30°，
又∵AB的垂直平分线DE分别交AB、BC于D、E，
∴AE=BE，
∴∠B=∠BAE=30°，
∴∠AEC=∠B+∠BAE=60°，
∴∠EAC=180°-∠C-∠AEC=90°，
∴△ACE为直角三角形，
则AE=BE=
CE.
故选：A.
练习册系列答案
相关题目
