Question

【题目】如图，在△ABC中，∠BAC的平分线与BC的中垂线DE交于点E，过点E作AC边的垂线，垂足为N，过点E作AB延长线的垂线，垂足为M.

(1)求证：BM=CN；

(2)若，AB=2，AC=8，求BM的长.

Answer 1

【答案】(1)证明见解析；（2）3.

【解析】

（1）因为ED是BC的垂直平分线，那么BE=CE，而AE是∠BAC的平分线，EM⊥AB，EN⊥AC，根据角平分线的性质可得EM=EN，再根据HL可判定Rt△BME≌Rt△CNE，从而有BM=CN．

（2）同（1）中方法证明Rt△AME≌Rt△ANE（HL），可得：AM=AN，又因为AM= AB+BM, AN= AC-CN，即可解答.

证明：连接BE，CE，如图，

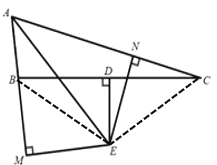
∴DE是BC的垂直平分线，
∴BE=CE，
∵AE是∠BAC的平分线，EM⊥AB，EN⊥AC，
∴EM=EN，
在Rt△BME和Rt△CNE中，

∴Rt△BME≌Rt△CNE（HL），
∴BM=CN

(2)由（1）得：EM=EN，

在Rt△AME和Rt△ANE中，

∴Rt△AME≌Rt△ANE（HL），
∴AM=AN，又∵AM= AB+BM, AN= AC-CN

∴AB+BM=AC-CN

∴2+ BM=8-CN, 又∵BM=CN

∴BM=CN =3