题目内容
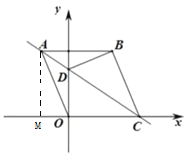
【题目】如图,四边形![]() 是菱形,以点
是菱形,以点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系.若点
轴建立平面直角坐标系.若点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() .
.
(1)求菱形![]() 的边长;
的边长;
(2)证明![]() 为直角三角形;
为直角三角形;
(3)直线![]() 上是否存在一点
上是否存在一点![]() 使得
使得![]() 的面积与
的面积与![]() 的面积相等?若存在,请求出点
的面积相等?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.


【答案】(1)13;(2)证明见解析;(3)![]() 为
为![]() 或
或![]() .
.
【解析】
(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,利用A点坐标及勾股定理即可求解;
,利用A点坐标及勾股定理即可求解;
(2)根据菱形的性质求出B,C点坐标,再求出AC的解析式,进而求出D点坐标,利用待定系数法求出直线BD,BC的解析式,根据k的值即可判断;
(3)根据△![]() 与
与![]() 的面积相等,故同底等高,于是延长BD交AO于P,即为所求,联立两直线的解析式即可求出P点坐标,再根据对称性求出另一点坐标.
的面积相等,故同底等高,于是延长BD交AO于P,即为所求,联立两直线的解析式即可求出P点坐标,再根据对称性求出另一点坐标.
解(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
![]() ,
,![]() ,
,
∴![]()
(2)∵![]() 为菱形,∴
为菱形,∴![]() ,
,
∴![]()
又∵![]() ,
,
∴![]()
又∵![]() ,
,
设直线AC的解析式为y=kx+b(k≠0)
把A,C代入得![]() ,
,
解得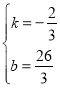 ,
,
∴![]() ,
,
令x=0,y=![]() ,
,
∴点![]()
设直线BC的解析式为y=px+q(p≠0)
把B,C代入得![]() ,
,
解得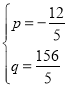 ,
,
∴![]() ,
,
设直线BD的解析式为y=mx+n(m≠0)
把B,D代入得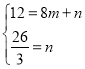 ,
,
解得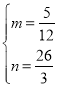 ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
所以![]() 为直角三角形;
为直角三角形;
(3)延长![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,
设直线AO的解析式为y=cx(c≠0),
把A代入得12=-5c,
解得c=![]() ,
,
∴![]() ,
,
由(2)知![]() 联立得:
联立得:
![]() ,
,
解得![]() ,
,
所以点![]() ,
,
作![]() 关于点
关于点![]() 的对称点
的对称点![]() ,
,
设P’(x,y),
可根据中点得: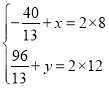 ,
,
解得 ,
,
∴![]() ,
,
综上点![]() 为
为![]() 或
或![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目