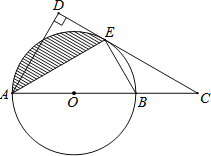
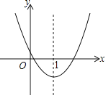
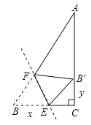
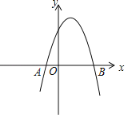
��Ŀ����
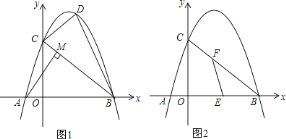
����Ŀ����ͼ![]() ����ƽ��ֱ������ϵ�У�ֱ��
����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �Ḻ������һ�㣬
�Ḻ������һ�㣬![]() �ڵ�
�ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ����֪������
����֪������![]() ������
������![]() ��
��![]() ��
��![]() ��
��
![]() �������ߵĺ�����ϵʽ��
�������ߵĺ�����ϵʽ��
![]() ����
����![]() ����
����![]() ���߶�
���߶�![]() �Ϸ����������ϣ�����
�Ϸ����������ϣ�����![]() ��
��![]() ����
����![]() ��
��![]() �������
�������![]() �����
�����![]() �����ꣻ
�����ꣻ
![]() ��ͼ
��ͼ![]() ��
��![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣨�����˵㣩������
��һ�㣨�����˵㣩������![]() ��һ����
��һ����![]() ��
��![]() ���������߶�
���������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���
����λ���ٶ��˶���![]() ���������߶�
���������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���
����λ���ٶ��˶���![]() ��ֹͣ������
��ֹͣ������![]() �������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��
�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��![]() �����꣮
�����꣮
���𰸡���1��![]() ��2��
��2��![]() ��
��![]() ��3����
��3����![]() �������˶����������õ�����ʱ��
�������˶����������õ�����ʱ��![]() �룬��ʱ��
�룬��ʱ��![]() ������Ϊ
������Ϊ![]()
��������
��1��������OC=3��4CN=5ON�����ON=![]() ����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A��-1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=-
����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A��-1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=-![]() x2+
x2+![]() x+3��
x+3��
��2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=-![]() x+3����PQ��y�ύBC��Q����ͼ1����P��x��-
x+3����PQ��y�ύBC��Q����ͼ1����P��x��-![]() x2+
x2+![]() x+3������Q��x��-
x+3������Q��x��-![]() x+3�����ټ����DQ=-
x+3�����ټ����DQ=-![]() x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=-
x2+3x�����������������ʽ��S��BCD=S��CDQ+S��BDQ=-![]() x2+6x��Ȼ�����S��BCD=
x2+6x��Ȼ�����S��BCD=![]() S��ABC�õ�-
S��ABC�õ�-![]() x2+6x=
x2+6x=![]() ��
��![]() ����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ
����4+1����3��Ȼ��ⷽ�����x���ɵõ�D�����ꣻ
��3����F��m��-![]() x+3�����������ľ��빫ʽ�õ�EF=
x+3�����������ľ��빫ʽ�õ�EF=![]() ��CF=
��CF=![]() x�����P�������˶�����������ʱ��t=EF+
x�����P�������˶�����������ʱ��t=EF+![]() =EF+
=EF+![]() CF�����ݲ���ʽ��ʽ�õ�EF+
CF�����ݲ���ʽ��ʽ�õ�EF+![]() CF��
CF��![]() ����EF=
����EF=![]() CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ��
CFʱ��ȡ�Ⱥţ���ʱt��С���ⷽ��![]() x2-
x2-![]() x+13=��
x+13=��![]()
![]() x��2��x1=2��x2=
x��2��x1=2��x2=![]() ����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2��
����ȥ�������ǵõ���P�������˶����������õ�����ʱ��2��![]() ��2=3�룬��ʱ��F������Ϊ��2��
��2=3�룬��ʱ��F������Ϊ��2��![]() ����
����
![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��
��![]() ��
��
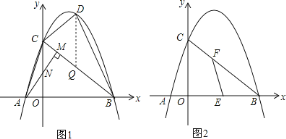
�������߽���ʽΪ![]() ��
��
��![]() �����
�����![]() �����
�����![]() ��
��
�������߽���ʽΪ![]() ��
��![]() ��ֱ��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() ��
��![]() �����
�����![]() �����
����� ��
��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() �ύ
�ύ![]() ��
��![]() ����ͼ
����ͼ![]() ����
����![]() ����
����![]() ��
��
![]() ��
��
��![]()
![]() ��
��
��![]() ��
��
��![]() ��
��
������![]() �����
�����![]() ��
��![]() ��
��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��![]() �������˶�����������ʱ��
�������˶�����������ʱ��![]() ����
����![]() ʱ��ȡ�Ⱥţ���ʱ
ʱ��ȡ�Ⱥţ���ʱ![]() ��С��
����
��![]() ��
��
������![]() �����
�����![]() ��
��![]() ����ȥ����
����ȥ����
���![]() �������˶����������õ�����ʱ��
�������˶����������õ�����ʱ��![]() �룬��ʱ��
�룬��ʱ��![]() ������Ϊ
������Ϊ![]() ��
��