题目内容
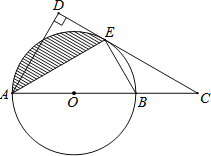
【题目】如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD于点D．
（1）求证：AE平分∠DAC；
（2）若AB=4，∠ABE=60°，求出图中阴影部分的面积．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）连接OE，可证得OE∥AD，则∠DAE=∠AEO=∠EAO，可得结论；
（2）由条件求得∠AOE=120°，容易求得△AOE和扇形AOE的面积，利用面积差可求得阴影部分的面积．
试题解析：（1）证明：连接OE，如图，
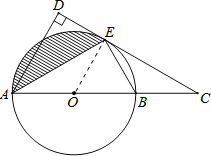
∵CD与⊙O相切于点E，
∴OE⊥CD，
∵AD⊥CD，
∴OE∥AD，
∴∠DAE=∠AEO，
∵AO=OE，
∴∠AEO=∠OAE，
∴∠OAE=∠DAE，
∴AE平分∠DAC；
（2）∵OA=OB，
∴∠AEO=∠OAE=30°，
∴∠AOE=120°，
∴阴影部分的面积=S扇形AOE﹣S△AOE
=S扇形AOE﹣
S△ABE
=
=．
练习册系列答案
相关题目
【题目】(1)填表：
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律：______________________________.
(3)根据你发现的规律填空：
①已知
=1.442,则
=__________,
=__________；
②已知
=0.076 96,则
=__________.
