Question

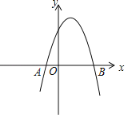
【题目】如图，在平面直角坐标系xOy中，已知抛物线y=﹣x2+2x+3与x轴交于A，B两点，点M在这条抛物线上，点P在y轴上，如果四边形ABMP是平行四边形，则点M的坐标为______．

Answer 1

【答案】（4，-5）.

【解析】

根据抛物线y=﹣x2+2x+3与x轴交于A，B两点，可求出A、B两点的坐标，进而求出AB的长度，由四边形ABMP是平行四边形，可知M点在x轴右边，PM//AB，且PM=AB=4 ，即可求出M点坐标.

∵y=﹣x2+2x+3与x轴交于A，B两点，

∴A（-1，0）；B（3，0）

∴AB=4，

∵四边形ABMP是平行四边形，

∴AB//PM，PM=AB=4，

∵P点在y轴上，

∴P点横坐标为4，

∵P点在抛物线y=﹣x2+2x+3上，

∴x=4时，y=-16+8+3=-5，

∴M点的坐标为：（4，-5）.

故答案为：（4，-5）