题目内容
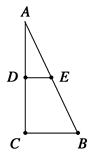
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,求折痕CE的长.


 .
.试题分析:先根据图形翻折变换的性质求出AC的长,再由勾股定理及等腰三角形的判定定理即可得出结论.
试题解析:∵△CEO是△CEB翻折而成,
∴BC=OC,BE=OE,
∵O是矩形ABCD的中心,
∴OE是AC的垂直平分线,AC=2BC=2×3=6,
∴AE=CE,
在Rt△ABC中,AC2=AB2+BC2,
即62=AB2+32,
解得AB=
 ,
,在Rt△AOE中,设OE=x,则AE=
 ,
,AE2=AO2+OE2,
即(
 )2=32+x2,
)2=32+x2,解得x=
 ,
,∴AE=EC=
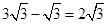 .
.考点: 1.翻折变换(折叠问题);2.矩形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目