题目内容
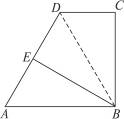
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为

| A.1 | B.2 | C.3 | D.4 |
C
本题考查了三角形中位线定理的运用,考查了三角形中位线定理的性质.
①将剪开的△ADE绕点E顺时针旋转180°,使EA和EB重合得到邻边不等的矩形;如图:
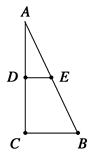
②将剪开的△ADE中的边AD和梯形DEBC中的边DC重合,△ADE中的边DE和梯形DEBC中的边BC共线,即可构成等腰梯形,如图:

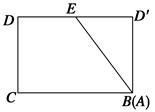
③将剪开的△ADE绕点D逆时针旋转180°,使得DA与DC重合,即可构成有一个角为锐角的菱形,如图:

故计划可拼出①②③.
故选C.
①将剪开的△ADE绕点E顺时针旋转180°,使EA和EB重合得到邻边不等的矩形;如图:

②将剪开的△ADE中的边AD和梯形DEBC中的边DC重合,△ADE中的边DE和梯形DEBC中的边BC共线,即可构成等腰梯形,如图:

③将剪开的△ADE绕点D逆时针旋转180°,使得DA与DC重合,即可构成有一个角为锐角的菱形,如图:

故计划可拼出①②③.
故选C.

练习册系列答案
相关题目

 折叠,使点
折叠,使点 与点
与点 重合,这时
重合,这时 为折痕,
为折痕, 为等腰三角形;再继续将纸片沿
为等腰三角形;再继续将纸片沿 折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
 为一边,画出一个斜三角形
为一边,画出一个斜三角形 ,使其顶点
,使其顶点
 沿
沿 折叠,使
折叠,使 点落在
点落在 边上的
边上的 点处;再将矩形
点处;再将矩形 折叠,使
折叠,使 点落在
点落在 点处且
点处且 过
过 点.
点.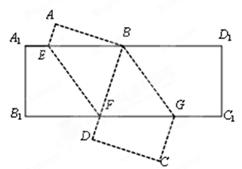
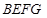 是平行四边形;
是平行四边形; 是多少度时,四边形
是多少度时,四边形