题目内容
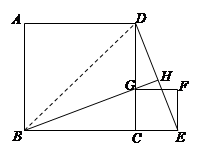
如图,已知正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.

(1)求证:①△BCG≌△DCE;②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.

(1)求证:①△BCG≌△DCE;②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
(1)见解析 (2)当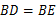 时,
时,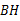 垂直平分
垂直平分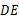 ,分析即可求得:
,分析即可求得: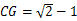 时,
时,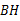 垂直平分
垂直平分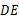
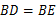 时,
时,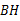 垂直平分
垂直平分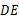 ,分析即可求得:
,分析即可求得: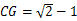 时,
时,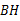 垂直平分
垂直平分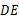
分析:(1)由四边形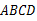 和四边形
和四边形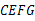 是正方形,根据正方形的性质,即可得
是正方形,根据正方形的性质,即可得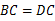 ,
, ,∠
,∠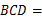 ∠
∠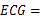 90°,则可根据SAS证得①△
90°,则可根据SAS证得①△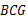 ≌△
≌△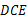 ;然后根据全等三角形的对应角相等,求得∠
;然后根据全等三角形的对应角相等,求得∠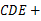 ∠
∠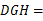 90°,则可得②
90°,则可得②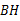 ⊥
⊥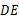 .
.
(2)当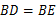 时,
时,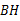 垂直平分
垂直平分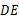 ,分析即可求得:
,分析即可求得: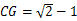 时,
时,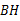 垂直平分
垂直平分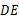 .
.
(1)证明:①∵ 四边形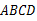 和四边形
和四边形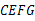 是正方形,
是正方形,
∴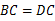 ,
, ,∠
,∠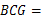 ∠
∠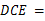 90°,
90°,
∴△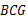 ≌△
≌△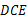 (SAS).
(SAS).
②∵△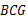 ≌△
≌△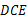 ,∴∠
,∴∠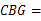 ∠
∠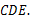
又∠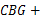 ∠
∠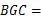 90°,
90°,
∴∠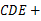 ∠
∠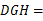 90°,
90°,
∴∠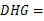 90°,∴
90°,∴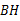 ⊥
⊥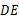 .
.
(2)解:当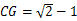 时,
时,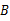 H垂直平分
H垂直平分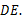
理由:如图,连接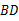 ,
,
∵ 四边形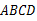 和四边形
和四边形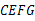 是正方形,
是正方形,
∴∠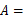 90°,
90°,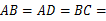 1,∴
1,∴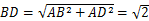 .
.
∵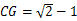 ,∴
,∴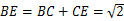 ,∴
,∴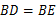 .
.
∵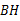 ⊥
⊥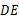 ,∴
,∴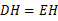 ,∴
,∴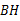 垂直平分
垂直平分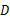 E,
E,
∴ 当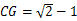 时,
时,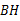 垂直平分
垂直平分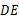 .
.
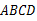 和四边形
和四边形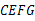 是正方形,根据正方形的性质,即可得
是正方形,根据正方形的性质,即可得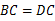 ,
, ,∠
,∠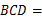 ∠
∠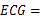 90°,则可根据SAS证得①△
90°,则可根据SAS证得①△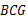 ≌△
≌△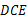 ;然后根据全等三角形的对应角相等,求得∠
;然后根据全等三角形的对应角相等,求得∠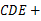 ∠
∠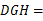 90°,则可得②
90°,则可得②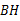 ⊥
⊥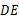 .
.(2)当
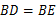 时,
时,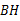 垂直平分
垂直平分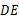 ,分析即可求得:
,分析即可求得: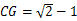 时,
时,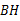 垂直平分
垂直平分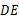 .
.(1)证明:①∵ 四边形
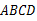 和四边形
和四边形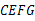 是正方形,
是正方形,∴
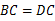 ,
, ,∠
,∠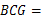 ∠
∠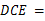 90°,
90°, ∴△
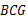 ≌△
≌△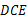 (SAS).
(SAS).②∵△
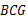 ≌△
≌△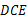 ,∴∠
,∴∠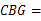 ∠
∠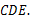
又∠
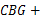 ∠
∠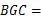 90°,
90°,∴∠
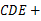 ∠
∠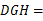 90°,
90°,∴∠
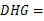 90°,∴
90°,∴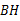 ⊥
⊥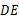 .
.(2)解:当
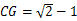 时,
时,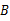 H垂直平分
H垂直平分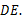
理由:如图,连接
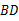 ,
,
∵ 四边形
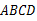 和四边形
和四边形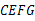 是正方形,
是正方形,∴∠
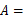 90°,
90°,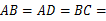 1,∴
1,∴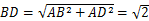 .
.∵
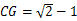 ,∴
,∴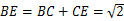 ,∴
,∴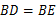 .
.∵
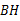 ⊥
⊥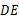 ,∴
,∴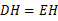 ,∴
,∴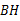 垂直平分
垂直平分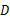 E,
E,∴ 当
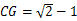 时,
时,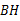 垂直平分
垂直平分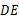 .
.
练习册系列答案
相关题目

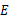 是正方形
是正方形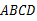 内一点,△
内一点,△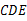 是等边三角形,连接
是等边三角形,连接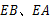 ,延长
,延长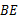 交边
交边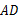 于点
于点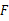 .
.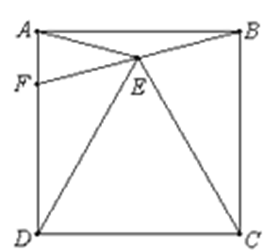
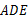 ≌△
≌△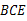 ;(2)求∠
;(2)求∠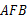 的度数.
的度数. 沿
沿 折叠,使
折叠,使 点落在
点落在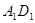 边上的
边上的 点处;再将矩形
点处;再将矩形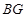 折叠,使
折叠,使 点落在
点落在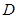 点处且
点处且 过
过 点.
点.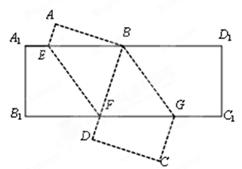
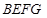 是平行四边形;
是平行四边形; 是多少度时,四边形
是多少度时,四边形 的周长为
的周长为 ,两条对角线相交于点
,两条对角线相交于点 ,且△
,且△ 的周长比△
的周长比△ 的周长大
的周长大 ,则
,则 的长为( )
的长为( )



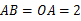 cm,则BD的长为________cm,BC的长为_______cm.(精确到0.1 cm)
cm,则BD的长为________cm,BC的长为_______cm.(精确到0.1 cm)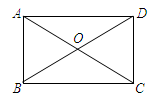
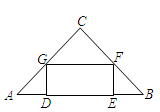
 ,AC = BC,AB = 30,矩形DEFG的一边DE在AB上,顶点G、F分别在AC、BC上,若DG︰GF = 1︰4,则矩形DEFG的面积是 .
,AC = BC,AB = 30,矩形DEFG的一边DE在AB上,顶点G、F分别在AC、BC上,若DG︰GF = 1︰4,则矩形DEFG的面积是 .