题目内容
在矩形ABCD中，AB=3,BC=4,则点A到对角线BD的距离为（ ）
A． | B．2 | C． | D． |
A.
试题分析：如图：
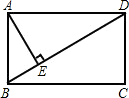
因为BC=4，故AD=4，AB=3，则S△DBC=
×3×4=6，又因为
，S△ABD=×5AE，故
×5AE=6，AE=．故选A．
考点: 矩形的性质
练习册系列答案
特高级教师点拨系列答案
文敬图书课时先锋系列答案
相关题目
试题分析：如图：
因为BC=4，故AD=4，AB=3，则S△DBC=
×3×4=6，又因为
，S△ABD=×5AE，故
×5AE=6，AE=．故选A．
考点: 矩形的性质
特高级教师点拨系列答案文敬图书课时先锋系列答案
折叠，使点
与点
重合，这时
为折痕，
为等腰三角形；再继续将纸片沿
折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”.
为一边，画出一个斜三角形
，使其顶点
是正方形
内一点，△
是等边三角形，连接
，延长
交边
于点
．
≌△
；（2）求∠
的度数．