题目内容
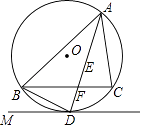
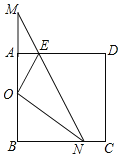
【题目】如图,已知Rt△MBN的两条直角边与正方形ABCD的两邻边重合,∠M=30°,O为AB中点,NO平分∠BNM,EO平分∠AEN.
(1)求证:△MON为等腰三角形;
(2)求证:EN=AE+BN.
【答案】(1)见解析;(2)见解析.
【解析】
(1) 根据三角形内角和定理、角平分线的性质和等角对等边证得站论.
(2)延长EO交CB的延长线于点P,构造全等三角形; △AOE≌△BOP,结合全等三角形的判定与性质进行解答.
(1)证明:∵∠B=90°,∠M=30°,
∴∠BNM=60°,
∵NO平分∠BNM,
∴∠ONM=![]() ∠BNM=30°,
∠BNM=30°,
∴∠ONM=∠M,
∴OM=ON,
∴MON为等腰三角形;
(2)证明:如图,延长EO交CB延长线于点P.
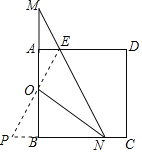
依题意得:∠BAE=∠ABP=90°.
∵O为AB中点,
∴OA=OB,
在△AOE和△BOP中,
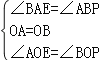 ,
,
∴△AOE≌△BOP(ASA),
∴AE=BP,OE=OP.
又NO平分∠BNM,
∴ON⊥EP,
∴EN=PN,
∴EN=PN=BP+BN=AE+BN,
∴EN=AE+BN.

练习册系列答案
相关题目