题目内容
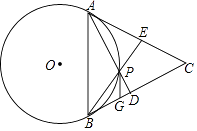
【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED; 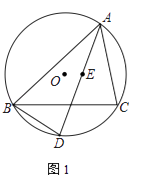
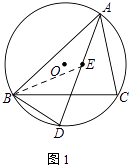
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC= ![]() ,求OE的长.
,求OE的长. 
【答案】
(1)证明:连接BE.
∵是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠DBC=∠CAD.
∴∠DBC=∠BAD.
∵∠BED=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴BD=ED.
(2)解:如图2所示;连接OB.

∵AD是直径,A平分∠BAC,
∴AD⊥BC,且BD=FC=3.
∵∠BAC=∠BOD,sin∠BAC= ![]() ,BF=3,
,BF=3,
∴OB=5.
∵在Rt△BOF中,BF=3,OB=5,
∴OF= ![]() =4.
=4.
∴DF=1.
在Rt△BDF中,BF2+DF2=BD2.
∴BD= ![]() .
.
∴DE= ![]() .
.
使用OE=5﹣ ![]() .
.
【解析】(1)连接BE.依据三角形的内心的性质以及圆周角定理证明∠DBE=∠DEB即可;(2)连接OB.先证明圆周角定理和三角形的内心的性质可知∠BAC=∠BOF,依据锐角三角函数的定义可求得OB的长,然后依据勾股定理可求得OF的长于是得到DF的长,接下来,在△BDF中,由勾股定理可求得BD的长,依据问题(1)的结论可得到DE的长,从而求得OE的长.

 智能训练练测考系列答案
智能训练练测考系列答案【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.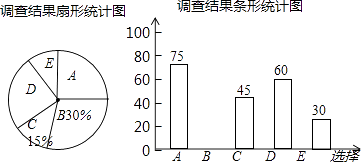
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.