题目内容
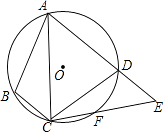
【题目】如图，四边形ABCD内接于⊙O，F是 
上一点，且 
= 
，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=110°，∠BAC=20°，则∠E的度数为（ ）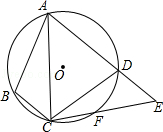 
A.60°
B.55°
C.50°
D.45°
【答案】C
【解析】解：∵四边形ABCD内接于⊙O，∠ABC=105°， ∴∠ADC=180°﹣∠ABC=180°﹣110°=70°．
∵且 
= 
，∠BAC=20°，
∴∠DCE=∠BAC=20°，
∴∠E=∠ADC﹣∠DCE=70°﹣20°=50°．
故选C．
【考点精析】利用圆心角、弧、弦的关系和圆内接四边形的性质对题目进行判断即可得到答案，需要熟知在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣，利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查．
造成医患关系紧张的原因（单选） |
根据调查结果绘制出了如下两幅尚不完整的统计图．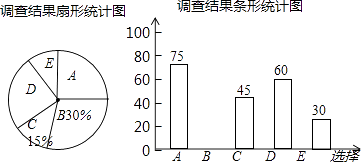
根据以上信息解答下列问题：
（1）这次接受调查的总人数为人；
（2）在扇形统计图中，“A”所在扇形的圆心角的度数为；
（3）补全条形统计图；
（4）若该市有1000万人，请你估计选D的总人数．
