ÌâÄ¿ÄÚÈİ
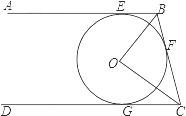
¡¾ÌâÄ¿¡¿£¨1£©Èçͼ 1£¬ÔÚ ABCD ÖĞ£¬AC¡¢BD ½»ÓÚµã O£¬¹ıµã O µÄÖ±Ïß l ½» AB ÓÚ E£¬ ½» CD ÓÚ F£¬¢ÙÅĞ¶Ï OE ºÍ OF µÄÊıÁ¿¹Øϵ£º £¬²¢Ö¤Ã÷£»
¢Ú SËıßĞÎAEFD SËıßĞÎCFEB £¨Ìî¡°>¡± »ò¡°=¡± »ò¡°<¡±£©£®
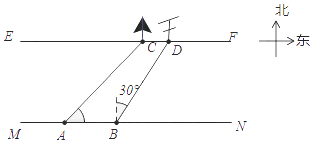
£¨2£©Èçͼ 2 ÊÇÒ»¿é¡°L¡±ĞεIJÄÁÏ£¬ÇëÄã×÷Ò»ÌõÖ±Ïß m£¬Ê¹µÃÖ±Ïß m Á½±ßµÄ²ÄÁϵÄÃæ»ıÏàµÈ£¨±£Áô×÷ͼºÛ¼££¬²»ÓÃÖ¤Ã÷£©£®
£¨3£©Èçͼ 3£¬Õı·½ĞÎ ABCD µÄ±ß³¤Îª 2![]() cm£¬¶¯µã P¡¢Q ·Ö±ğ´Óµã A¡¢C ͬʱ³ö·¢£¬ÒÔ ÏàͬµÄËٶȷֱğÑØ AD¡¢CB ÏòÖÕµã D¡¢B Òƶ¯£¬µ±µã P µ½´ïµã D ʱ£¬Ô˶¯Í£Ö¹£¬¹ıµã C ×÷ CH¡ÍPQ£¬´¹×ãΪµã H£¬Á¬½Ó BH£¬Ôò BH ³¤µÄ×îСֵΪ cm£¨±£Áô×÷ͼºÛ¼££¬ Ö±½ÓÌîĞ´½á¹û£©£®
cm£¬¶¯µã P¡¢Q ·Ö±ğ´Óµã A¡¢C ͬʱ³ö·¢£¬ÒÔ ÏàͬµÄËٶȷֱğÑØ AD¡¢CB ÏòÖÕµã D¡¢B Òƶ¯£¬µ±µã P µ½´ïµã D ʱ£¬Ô˶¯Í£Ö¹£¬¹ıµã C ×÷ CH¡ÍPQ£¬´¹×ãΪµã H£¬Á¬½Ó BH£¬Ôò BH ³¤µÄ×îСֵΪ cm£¨±£Áô×÷ͼºÛ¼££¬ Ö±½ÓÌîĞ´½á¹û£©£®

¡¾´ğ°¸¡¿£¨1£©¢ÙOE£½OF£¬Ö¤Ã÷¼ûÏê½â£»¢Ú£½£»£¨2£©´ğ°¸¼ûÏê½â£»£¨3£©![]()
¡¾½âÎö¡¿
£¨1£©¢Ùͨ¹ıÖ¤Ã÷¡÷AOE¡Õ¡÷COF¼´¿ÉÅжÏOE£¬OFµÄÊıÁ¿¹Øϵ£»
¢ÚÀûÓÃƽĞĞËıßĞκÍÈ«µÈÈı½ÇĞεÄĞÔÖʵõ½![]() £¬
£¬![]() £¬È»ºóÀûÓõÈʽµÄĞÔÖÊÇó½â£»
£¬È»ºóÀûÓõÈʽµÄĞÔÖÊÇó½â£»
£¨2£©Ö±½ÓÀûÓþØĞεÄĞÔÖʽáºÏÖĞĞĶԳÆͼĞεÄĞÔÖʵóö´ğ°¸£»
£¨3£©ÉèÕı·½ĞεÄÖĞĞÄΪO£¬¿ÉÖ¤PQ¾¹ıOµã£®Á¬½áOC£¬È¡OCÖеãM£¬Á¬½á MH£¬MB£¬ÀûÓÃÕı·½ĞεÄĞÔÖʺ͹´¹É¶¨ÀíÇó³öMBµÄ³¤£¬ÀûÓÃÖ±½ÇÈı½ÇĞÎб±ßÖĞÏßµÈÓÚб±ßÒ»°ëÇó³öMHµÄ³¤£¬È»ºóÀûÓÃÁ½µãÖ®¼äÏ߶Î×î¶Ì½â¾öÎÊÌâ¼´¿É£®
½â£º£¨1£©¢Ù¡ßËıßĞÎABCDÊÇƽĞĞËıßĞΣ¬
¡àAO=OC£¬AB¡ÎCD£¬
¡à¡ÏEAO=¡ÏFCO£¬
ÔÚ¡÷EAOºÍ¡÷FCOÖĞ£¬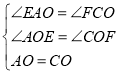
¡à¡÷AOE¡Õ¡÷COF
¡àOE=OF
¹Ê´ğ°¸Îª£ºOE=OF£»
¢Ú¡ßÔÚ ABCD ÖĞ£¬![]()
ÓÖÓÉ¢Ù¿ÉÖª¡÷AOE¡Õ¡÷COF
¡à![]()
¡à![]()
¼´SËıßĞÎAEFD=SËıßĞÎCFEB
¹Ê´ğ°¸Îª£º=£»

£¨2£©ÈçͼËùʾ£º
ÏÈÕÒµ½Á½¸ö¾ØĞεÄÖĞĞÄ£¬È»ºóÁ¬½ÓÖĞĞÄ
Ö±Ïßm¼´ÎªËùÇó

£¨3£©ÉèÕı·½ĞεÄÖĞĞÄΪO£¬
ÓÉÌâÒâ¿ÉÖªPD=BQ
¡àÔÚÕı·½ĞÎABCDÖĞ¿ÉÖªPQ¾¹ıOµã£®
Á¬½áOC£¬È¡OCÖеãM£¬Á¬½á MH£¬MB£¬
¡ßÕı·½ĞÎ ABCD µÄ±ß³¤Îª 2![]() cm
cm
¡àCO=BO=![]() £¬OM=MC=
£¬OM=MC=![]()
¡à![]()
¡ßCH¡ÍPQ
¡àMH=![]()
BH¡İBM-MH
¼´BH¡İ![]()
¡àµ±B£¬H£¬MÈıµã¹²Ïßʱ£¬BH×îСΪ![]()
¹Ê´ğ°¸Îª£º![]() £®
£®


 Сѧ½Ì²ÄÈ«²âϵÁĞ´ğ°¸
Сѧ½Ì²ÄÈ«²âϵÁĞ´ğ°¸ СѧÊıѧ¿ÚËãÌ⿨ÍÑ¿Ú¶ø³öϵÁĞ´ğ°¸
СѧÊıѧ¿ÚËãÌ⿨ÍÑ¿Ú¶ø³öϵÁĞ´ğ°¸ ÓÅĞãÉúÓ¦ÓÃÌ⿨¿ÚËãÌìÌìÁ·ÏµÁĞ´ğ°¸
ÓÅĞãÉúÓ¦ÓÃÌ⿨¿ÚËãÌìÌìÁ·ÏµÁĞ´ğ°¸ Õã½Ö®ĞÇ¿ÎʱÓÅ»¯×÷ҵϵÁĞ´ğ°¸
Õã½Ö®ĞÇ¿ÎʱÓÅ»¯×÷ҵϵÁĞ´ğ°¸