题目内容
【题目】已知⊙O的半径为13,弦AB//CD,AB=24,CD=10,则AB、CD之间的距离为( )
A.17
B.7
C.12
D.7或17
【答案】D
【解析】①当弦AB和CD在圆心同侧时,如图1,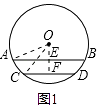
过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12﹣5=7cm;
②当弦AB和CD在圆心异侧时,如图2, 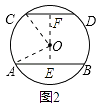
过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm,
∴AB与CD之间的距离为7cm或17cm.
故答案为:D.
此题分两种情况:①当弦AB和CD在圆心同侧时,如图1,过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,根据垂径定理得出AE=12cm,CF=5cm,根据勾股定理得出EO=5cm,OF=12cm,然后根据EF=OE-OF算出答案;②当弦AB和CD在圆心异侧时,如图2, 过点O作OE⊥AB于点E,OF⊥CD于点F ,连接OA,OC ,根据垂径定理得出AE=12cm,CF=5cm,根据勾股定理得出EO=5cm,OF=12cm,然后根据EF=OE+OF算出答案 .

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目