题目内容
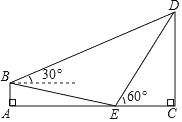
【题目】已知,△ABC中,∠ACB=90°,AC=BC=8,点A在半径为5的⊙O上,点O在直线l上.
(1)如图①,若⊙O经过点C,交BC于点D,求CD的长.
(2)在(1)的条件下,若BC边交l于点E,OE=2![]() ,求BE的长.
,求BE的长.
(3)如图②,若直线l还经过点C,BC是⊙O 的切线,F为切点,则CF的长为____.
【答案】(1)CD=6;(2)BE=5-2![]() ;(3)4.
;(3)4.
【解析】
(1)由圆周角定理可得AD是直径,根据勾股定理可求CD的长;
(2)过点O作OF⊥CD,垂足为F,根据垂径定理可得CF=DF=3,根据中位线定理可得OF=4,根据勾股定理可求EF的长,即可求BE的长;
(3)连接OF,OA,过点O作OE⊥AC于点E,可证四边形OECF是矩形,可得CF=OE,FO=CE=5,由勾股定理可求AE的长,即可求CF的长.
解:(1)如图:连接AD
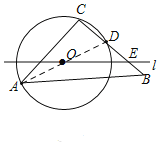
∵∠ACB=90°,
∴AD是直径
∴AD=10
在Rt△ACD中,CD![]() =6
=6
(2)如图:过点O作OF⊥CD,垂足为F

∵OF⊥CD
∴CF=DF=3,且AO=DO
∴OF=![]() AC=4
AC=4
在Rt△OFE中,EF=![]()
∵BE=BC-CF-EF
∴BE=8-3-![]()
(3)如图:连接OF,OA,过点O作OE⊥AC于点E,
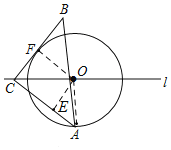
∵BC是⊙O 的切线
∴OF⊥BC,
∴∠BFO=∠ACB=90°,OE⊥CE,
∴四边形OECF是矩形
∴CF=OE,FO=CE=5,
∴AE=AC-CE=3
在Rt△AEO中,OE=![]() =4,
=4,
∴CF=4
故答案为:4

【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.