��Ŀ����
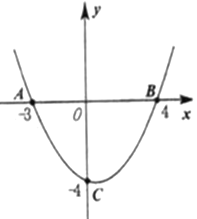
����Ŀ�������Ǵ��ϲ���ּ���һ�������˶�,��������ʱ,��Ҫ����ͬƵ˦������,������˦����ߴ�ʱ,����״�ɽ��ƿ���������,��ͼ��С����С��˦���ӵ���ߴ�ʱ��ʾ��ͼ,���������ӵ���֮��ľ���Ϊ4![]() ,�����ĸ߶�Ϊ1
,�����ĸ߶�Ϊ1![]() ,��С����������λ��Ϊԭ�㽨��ƽ��ֱ������ϵ.
,��С����������λ��Ϊԭ�㽨��ƽ��ֱ������ϵ.
(1)������Ϊ15![]() ��С��վ�����ӵ����·�,�Ҿ�С���������ֵ��Ҳ�1
��С��վ�����ӵ����·�,�Ҿ�С���������ֵ��Ҳ�1![]() ��ʱ,���Ӹպ�ͨ��С���ͷ��,����������Ӧ�������ߵı���ʽ;
��ʱ,���Ӹպ�ͨ��С���ͷ��,����������Ӧ�������ߵı���ʽ;
(2)������Ϊ![]() ��С��Ҳվ�����ӵ����·�.
��С��Ҳվ�����ӵ����·�.
�ٵ�С���ھ�С���������ֵ����1.5![]() ��ʱ,����������С����ͷ��?��˵�����ɣ�
��ʱ,����������С����ͷ��?��˵�����ɣ�
����С����С����������֮���ˮƽ����Ϊ![]() ,Ϊ��֤���Ӳ�����С����ͷ��,��
,Ϊ��֤���Ӳ�����С����ͷ��,��![]() ��ȡֵ��Χ.(�ο�����:
��ȡֵ��Χ.(�ο�����: ![]() ȡ3.16)
ȡ3.16)

���𰸡���1��![]() ����2��������������С����ͷ�����ɼ���������
����2��������������С����ͷ�����ɼ���������![]() .
.
��������
��1����Ϊ�����߹�ԭ�㣬���������ߵĽ���ʽΪ��y=ax2+bx��a��0������С�������ӵ��ֵ����꣨4��0�����Լ�С��ͷ�����꣨1��1.5-1�����룬�õ���Ԫһ�η����飬�ⷽ�����ɣ�
��2�������Ա�����ֵ�������ֵ���ٱȽϱ�ɣ�����y=0.65ʱ������Ա�����ֵ�����ȷ��d��ȡֵ��Χ��
��1����������,����������Ӧ�������ߵı���ʽΪ![]()
��![]() ��
��
�������߾�����![]() �͵�
�͵�![]()
��![]() �����
�����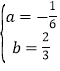
�����Ӷ�Ӧ�������߱���ʽΪ![]()
��2��������������С����ͷ
�������£�
��С���ھ�С���������ֵ����1.5![]() ����
����
��С������λ����ԭ�����Ϊ![]() ��
��
�൱![]() ʱ��
ʱ��![]()
��![]()
������������С����ͷ.
�ڡ�1.65-1=0.65���൱![]() ʱ��
ʱ��![]()
��![]() ����ã�
����ã�![]()
��![]() ȡ3.16
ȡ3.16
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() .
.