��Ŀ����
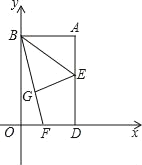
����Ŀ����ͼ���ı���ABCDΪ���Σ�AB��4cm��AD��3cm������M��N�ֱ�ӵ�D��Bͬʱ����������1cm/s���ٶ��˶�����M��DA���յ�A�˶�����N��BC���յ�C�˶�������N��NP��BC����AC�ڵ�O������MP����֪�����˶���ts��0��t��3����
��1����tΪ����ʱ��PM��AB��
��2�����ı���CDMP�����ΪS������S��t�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��tʹ�ı���CDMP������ı���ABCD�����Ϊ3��8�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��4���ڵ�M��N�˶������У���MPA�ܷ��Ϊһ�����������Σ����ܣ�������п��ܵ�tֵ�������ܣ���˵�����ɣ�

���𰸡���1����t=![]() ʱ��PM��AB����2��s��
ʱ��PM��AB����2��s��![]() t2��2t+6����3��t��
t2��2t+6����3��t��![]() ʱ�ı���CDMP��������ı���ABCD�������Ϊ3��8����4����t��1��t��
ʱ�ı���CDMP��������ı���ABCD�������Ϊ3��8����4����t��1��t��![]() ��t��
��t��![]() ʱ����MPA�ǵ��������Σ�
ʱ����MPA�ǵ��������Σ�
��������
��1��������֪�����õ�PM��PN��ֱ�ߣ����MN��AB���з��̼��ɵõ����ۣ�
��2���ӳ�NP��AD�ڵ�Q����PQ��AD������PNC�ס�ABC��![]() ��
��![]() ����S�ı���CDMP��S��ACD��S��AMP�ɵã�
����S�ı���CDMP��S��ACD��S��AMP�ɵã�
��3����![]() �ⷽ�̿ɵã�
�ⷽ�̿ɵã�
��4������Ҫ�������������MP��PA����ôAQ��BN��![]() AM������x�ֱ��ʾ��BN��AM�ij���Ȼ���������������ϵ�����x��ֵ����MA��MP����ֱ��������MQP�У�MQ��MA��BN��PQ��AB��PN���ݹ��ɶ����������x��ֵ����MA��PA�����ѵó�AP��
AM������x�ֱ��ʾ��BN��AM�ij���Ȼ���������������ϵ�����x��ֵ����MA��MP����ֱ��������MQP�У�MQ��MA��BN��PQ��AB��PN���ݹ��ɶ����������x��ֵ����MA��PA�����ѵó�AP��![]() BN��Ȼ����x��ʾ��AM�ij����������x��ֵ��
BN��Ȼ����x��ʾ��AM�ij����������x��ֵ��
�⣺��1����PM��AB��AB��PN��
��PM��PN��ֱ�ߣ�
��MN��AB��
��AM��NB��
��3��t��t��
��![]()
��2����ͼ���ӳ�NP��AD�ڵ�Q����PQ��AD��

������֪��DM��BN��t��AM��CN��3��t��
��PN��AB��
���PNC�ס�ABC��
��![]() ��
��![]()
��ã� ![]()
��PQ��AD��
���QAB����B����NQA��90����
���ı���ABNQ�Ǿ��Σ�
��AB��QN��4��
��![]()
���ı���CDMP�����![]()
��3����S����ABCD��3��4��12��
��![]()
��ã�![]()
����![]() ʱ�ı���CDMP��������ı���ABCD�������Ϊ3��8��
ʱ�ı���CDMP��������ı���ABCD�������Ϊ3��8��
��4����MPA�ܳ�Ϊ���������Σ�����������������·���˵����
����PM��PA��
��PQ��MA��
���ı���ABNQ�Ǿ��Σ�
��QA��NB��t��
��MQ��QA��t��
�֡�DM+MQ+QA��AD
��3t��3����t��1
����MP��MA����MQ��3��2t��![]() MP��MA��3��t��
MP��MA��3��t��
��Rt��PMQ�У��ɹ��ɶ����ã�MP2��MQ2+PQ2
��![]()
��ã�t��![]() ��t��0�������⣬��ȥ��
��t��0�������⣬��ȥ��
����AP��AM��
������ɵã�AP��![]() t��AM��3��t
t��AM��3��t
��![]()
��ã�t��![]() ��
��
������������t��1��t��![]() ��t��
��t��![]() ʱ����MPA�ǵ��������Σ�
ʱ����MPA�ǵ��������Σ�