题目内容
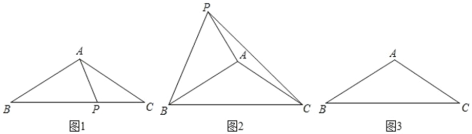
【题目】如图,在平面直角坐标系中,已知点A(0,4),△AOB为等边三角形,P是x轴负半轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由;
(3)连接OQ,当OQ∥AB时,求点P的坐标.
【答案】(1)B(![]() );(2)∠ABQ=90°,始终不变,理由详见解析;(3)P(
);(2)∠ABQ=90°,始终不变,理由详见解析;(3)P(![]() )
)
【解析】
(1)过点B作BC⊥x轴于点C,证明∠BOC=30°,OB=4,借助含30°的直角三角形的性质以及勾股定理可求出BC,OC的长,从而可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题;
(3)根据AB∥OQ,得出∠BQO=90°,∠BOQ=∠ABO=60°,从而可求出BQ的长,再根据(2)中△APO≌△AQB得出PO=BQ,即可得出结果.
解:(1)如图1,过点B作BC⊥x轴于点C,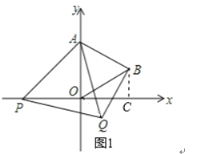
∵△AOB为等边三角形,且OA=4,
∴∠AOB=60°,OB=OA=4,
∴∠BOC=30°,而∠OCB=90°,
∴BC=![]() OB=2,∴OC=
OB=2,∴OC=![]() ,
,
∴点B的坐标为B(2![]() ,2);
,2);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ,AO=AB,∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,
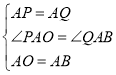 ,
,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)如图2,∵点P在x轴负半轴上,点Q在点B的下方,AB∥OQ,∠ABQ=90°,
∴∠BQO=90°,∠BOQ=∠ABO=60°,
∴∠OBQ=30°,
又∵OB=4,
∴OQ=2,
∴BQ=![]() ,
,
由(2)可知,△APO≌△AQB,
∴OP=BQ=2![]() ,
,
∴此时点P的坐标为(-2![]() ,0).
,0).

【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
数据段 | 频数 | 频率 |
30~40 | 10 | 0.05 |
40~50 | 36 | |
50~60 | 0.39 | |
60~70 | ||
70~80 | 20 | 0.10 |
总计 | 200 | 1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
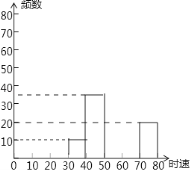
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?