Question

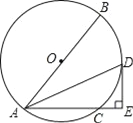
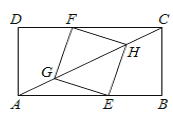
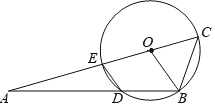
【题目】如图，以△AOB 的顶点 O 为圆心，OB 为半径作⊙O，交 OA 于点 E，交 AB 于点 D，连接 DE，DE∥OB，延长 AO 交⊙O 于点 C，连接 CB．

(1)求证：；

(2)若 AD＝4，AE＝CE，求 OC 的长．

Answer 1

【答案】(1)证明见解析；(2)OC =3．

【解析】

（1）连接 CD 交 OB 于 F，推出OB⊥CD，推出 ，

即BC=BD；

（2）连接 CD 交 OB 于 F，连接 EF，推出四边形 EFBD 是平行四边形，设 OF＝x，列出关于x的方程，解出其值，即可得出OC的值.

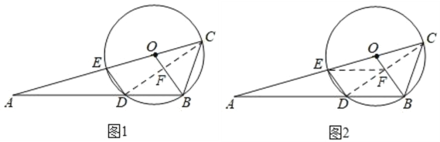
如图 1，连接 CD 交 OB 于 F，

∵CE 是直径，

∴∠EDC＝90°，

∵DE∥OB，

∴∠EDC＝∠OFC＝90°， 即 OB⊥CD，

∴；

如图 2，连接 CD 交 OB 于 F，连接 EF，

由(1)得：DE∥OB，OB⊥CD，点 F 是 CD 的中点，

∵AE＝CE，

∴EF∥AD，EF＝ AD＝2 ，

∵O 是 CE 的中点，F 是 CD 的中点，

∴OF＝ DE，

∵EF∥BD，DE∥BF，

∴四边形 EFBD 是平行四边形，

∴BF＝DE，

设 OF＝x，则 BF＝DE＝2x，OC＝OB＝3x，

∵，

∴BC＝BD＝EF＝2 ，

∵DF2＝CF2

∴，

解得：x＝±1，

∵x＞0，

∴x＝1，

∴OC＝3x＝3．