Question

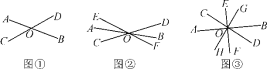
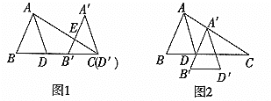
【题目】如图1，平移三角形ABD，使点D沿BD的延长线平移至点C，得到三角形△A'B'D'，A'B'交AC于点E，AD平分∠BAC．

（1）猜想∠B'EC与∠A'之间的关系，并写出理由；

（2）如果将三角形ABD平移至如图2所示位置，得到△A'B'D'，请问：A'D'平分∠B'A'C吗？为什么？

Answer 1

【答案】（1）∠B'EC=2∠A'；理由见解析；（2）A'D'平分∠B'A'C，理由见解析.

【解析】

（1）根据角平分线的性质得出∠BAD=∠DAC，根据平移的性质得出∠BAD=∠A'，AB∥A'B'，进而得出∠BAC=∠B'EC，即可得出答案；

（2）利用平移的性质得出∠B'A'D'=∠BAD，AB∥A'B'，进而得出∠BAD∠BAC，即可得出∠B'A'D'∠B'A'C．

（1）∠B'EC=2∠A'．理由如下：

∵AD平分∠BAC，∴∠BAD=∠DAC．

∵将△ABD平移，使D沿BD延长线移至C得到△A'B'D'，A'B'交AC于E，∴∠BAD=∠A'，AB∥A'B'，∴∠BAC=∠B'EC，∴∠BAD=∠A'∠BAC∠B'EC，即∠B'EC=2∠A'；

（2）A'D'平分∠B'A'C．理由如下：

∵将△ABD平移至如图（2）所示，得到△A'B'D'，∴∠B'A'D'=∠BAD，AB∥A'B'，∴∠BAC=∠B'A'C．

∵∠BAD∠BAC，∴∠B'A'D'∠B'A'C，∴A'D'平分∠B'A'C．