题目内容
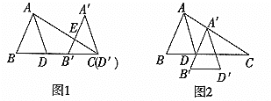
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
【答案】解:(1)证明:∵在△CBF和△DBG中,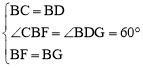 ,
,
∴△CBF≌△DBG(SAS)。
∴CF=DG。
(2)∵△CBF≌△DBG,∴∠BCF=∠BDG。
又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°。
∴∠FHG=180°﹣∠DHF=180°﹣60°=120°。
【解析】
试题(1)在△CBF和△DBG中,根据SAS即可证得两个三角形全等,根据全等三角形的对应边相等即可证得。
(2)根据全等三角形的对应角相等,即可证得∠DHF=∠CBF=60°,从而求解。

【题目】九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
售价(元/本) | 50 | 55 | 60 | 65 | … |
月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是元,②月销量是件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
【题目】为了合理利用电力资源,缓解用电紧张状况,我国电力部门出台了使用“峰谷电”的政策及收费标准(见下表).
用电时间段 | 收费标准 | |
峰电 | 08:00—22:00 | 0.56元/千瓦时 |
谷电 | 22:00—08:00 | 0.28元/千瓦时 |
已知王老师家4月份使用“峰谷电”95千瓦时,缴电费43.40元,问王老师家4月份“峰电”和“谷电”各用了多少千瓦时?设王老师家4月份“峰电”用了x千瓦时,“谷电”用了y千瓦时,根据题意,列方程组得_____.