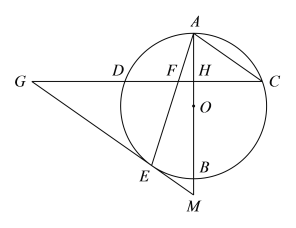
题目内容
【题目】如图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.

(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(3,1),在此坐标系下,B点的坐标为 ;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为 ;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c的图象过O、B、C三点,D为此抛物线的顶点。试求出抛物线解析式及D点的坐标。
【答案】(1)建立坐标系详见解析,(1,2);(2)线段BC详见解析,(2,0); (3)![]() ,D(1,
,D(1,![]() ).
).
【解析】
(1)建立坐标系如图,满足A点坐标为(-3,-1),在此坐标系下,得到B点坐标;
(2)在(1)图中作出线段BC,求出C点坐标;
(3)将O、B、C三点坐标代入二次函数解析式中,解方程得到二次函数的解析式,将所求的二次函数的解析式化简,求出顶点D的坐标.
(1)建立坐标系如图,
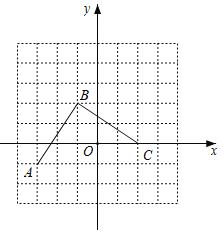
∴B点的坐标为(1,2);
故答案为:(1,2);
(2)线段BC如图所示,
C点的坐标为(2,0);
故答案为:(2,0);
(3)∵C点的坐标为(2,0),O(0,0),B(1,2)
∴所求二次函数解析式为![]()
∴![]()
∴D(1,![]() )
)

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目