题目内容
如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,作∠ABC的平分线交AC、CD于点E、F.
(1)求证:CE=CF;
(2)如图2,过点F作FG∥AB交AC于点G,若AC=10,EG=4,求CE的长度.
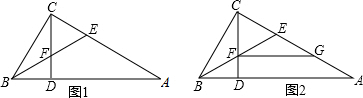
(1)求证:CE=CF;
(2)如图2,过点F作FG∥AB交AC于点G,若AC=10,EG=4,求CE的长度.

分析:(1)根据直角三角形的两锐角互余可知∠CBE+∠BEC=90°,∠BFD+∠DBF=90°,再根据角平分线的定义可知∠CBE=∠DBF,从而求出∠BFD=∠BEC,又对顶角相等,然后根据等角对等边可得CE=CF;
(2)过点G作GM⊥AD于点M,过点F作FN⊥BC于点N,根据角平分线上的点到角的两边距离相等可得FD=NF,然后证明四边形GFDM是矩形,根据矩形的对边相等可得GM=DF,然后利用角角边证明△AGM与△CFN全等,根据全等三角形对应边相等可得CF=AG,从而可得AG=CE,然后利用AC=CE+EG+AG代入数据求解即可.
(2)过点G作GM⊥AD于点M,过点F作FN⊥BC于点N,根据角平分线上的点到角的两边距离相等可得FD=NF,然后证明四边形GFDM是矩形,根据矩形的对边相等可得GM=DF,然后利用角角边证明△AGM与△CFN全等,根据全等三角形对应边相等可得CF=AG,从而可得AG=CE,然后利用AC=CE+EG+AG代入数据求解即可.
解答:(1)证明:∵∠ACB=90°,CD⊥AB,
∴∠CBE+∠BEC=90°,∠BFD+∠DBF=90°,
∵BE是∠ABC的平分线,
∴∠CBE=∠DBF,
∴∠BFD=∠BEC,
又∵∠BFD=∠CFE(对顶角相等),
∴∠BEC=∠CFE,
∴CE=CF;
(2)解:如图,过点G作GM⊥AD于点M,过点F作FN⊥BC于点N,
则∠CNF=∠AMG=90°,
∵BE是∠ABC的平分线,CD⊥AB,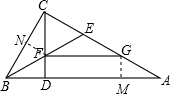
∴FD=NF,
又∵FG∥AB,
∴四边形GFDM是矩形,
∴GM=DF,
∴GM=NF,
∵∠A+∠ABC=90°,∠BCD+∠ABC=90°,
∴∠A=∠BCD,
在△AGM与△CFN中,
,
∴△AGM≌△CFN(AAS),
∴CF=AG,
根据(1)可知CE=CF,
∴CE=AG,
∵AC=10,EG=4,
∴CE+EG+AG=2CE+4=10,
解得CE=3.
∴∠CBE+∠BEC=90°,∠BFD+∠DBF=90°,
∵BE是∠ABC的平分线,
∴∠CBE=∠DBF,
∴∠BFD=∠BEC,
又∵∠BFD=∠CFE(对顶角相等),
∴∠BEC=∠CFE,
∴CE=CF;
(2)解:如图,过点G作GM⊥AD于点M,过点F作FN⊥BC于点N,
则∠CNF=∠AMG=90°,
∵BE是∠ABC的平分线,CD⊥AB,

∴FD=NF,
又∵FG∥AB,
∴四边形GFDM是矩形,
∴GM=DF,
∴GM=NF,
∵∠A+∠ABC=90°,∠BCD+∠ABC=90°,
∴∠A=∠BCD,
在△AGM与△CFN中,
|
∴△AGM≌△CFN(AAS),
∴CF=AG,
根据(1)可知CE=CF,
∴CE=AG,
∵AC=10,EG=4,
∴CE+EG+AG=2CE+4=10,
解得CE=3.
点评:本题考查了角平分线的性质,全等三角形的判定与性质,(2)中作辅助线构造出全等三角形求出CE=AG是解题的关键,也是本题的难点.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目