题目内容
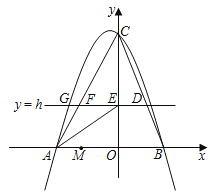
【题目】如图,△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:
①作∠BAC的平分线AM交BC于点D;
②作边AB的垂直平分线EF,EF与AM相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(1)线段PA,PB,PC之间的数量关系是 ;
(2)若∠ABC=70°,求∠BPC的度数.

【答案】(1)PA=PB=PC;(2)80°.
【解析】
(1)根据线段的垂直平分线的性质可得:PA=PB=PC;
(2)根据等腰三角形的性质得:∠ABC=∠ACB=70°,由三角形的内角和得:∠BAC=180°﹣2×70°=40°,由角平分线定义得:∠BAD=∠CAD=20°,最后利用三角形外角的性质可得结论.
(1)如图,PA=PB=PC,理由是:
∵AB=AC,AM平分∠BAC,
∴AD是BC的垂直平分线,
∴PB=PC,
∵EP是AB的垂直平分线,
∴PA=PB,
∴PA=PB=PC;
故答案为:PA=PB=PC;
(2)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°﹣2×70°=40°,
∵AM平分∠BAC,
∴∠BAD=∠CAD=20°,
∵PA=PB=PC,
∴∠ABP=∠BAP=∠ACP=20°,
∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°.

【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛. 并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级:A:优秀,B:良好,C:一般,D:较差),并制作了如下统计图表(部分信息未给出):
等级 | 人数 |
A | m |
B | 20 |
C | n |
D | 10 |

请根据统计图表中的信息解答下列问题:
(1)这次共抽取了________名参加演讲比赛的学生,统计图中a=________,b=________;
(2)若该校学生共有2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的有多少人?
(3)若演讲比赛成绩为A等级的学生中恰好有2名女生,其余的学生为男生,从A等级的学生中抽取两名同学参加全市演讲比赛,求抽中一名男生和一名女生的概率.