题目内容
【题目】如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.
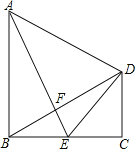
(1)求证:△ABE≌△BCD;
(2)判断线段AE与BD的数量关系及位置关系,并说明理由;
(3)若CD=1,试求△AED的面积.
【答案】(1)见解析;(2)AE=BD,AE⊥BD,理由见解析;(3)△AED的面积为![]() .
.
【解析】
(1)由已知条件可推导得到![]() ,由SAS即可证明△ABE≌△BCD;
,由SAS即可证明△ABE≌△BCD;
(2)由(1)可得△ABE≌△BCD 可得AE=BD,再由角的转化可得∠AFB=90°,即可证明AE⊥BD;
(3)因为 △AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可求解△AED的面积.
(1)证明:∵AB∥CD,
∴∠ABE+∠C=180°,
∵∠C=90°,
∴∠ABE=90°=∠C,
∵E是BC的中点,
∴BC=2BE,
∵BC=2CD,
∴BE=CD,
在△ABE和△BCD中,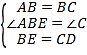 ,
,
∴△ABE≌△BCD(SAS);
(2)解:AE=BD,AE⊥BD,理由如下:
由(1)得:△ABE≌△BCD,
∴AE=BD,
∵∠BAE=∠CBD,∠ABF+∠CBD=90°,
∴∠ABF+∠BAE=90°,
∴∠AFB=90°,
∴AE⊥BD;
(3)解:∵△ABE≌△BCD,
∴BE=CD=1,
∵AB=BC=2CD=2,
∴CE=BC﹣BE=1,
∴CE=CD,
∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=![]() (1+2)×2﹣
(1+2)×2﹣![]() ×2×1﹣
×2×1﹣![]() ×1×1=
×1×1=![]()

练习册系列答案
相关题目