Question

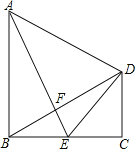
【题目】如图，四边形中，，，，设的长为，四边形的面积为，则与之间的函数关系式是（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

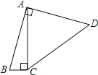
四边形ABCD图形不规则，根据已知条件，将△ABC绕A点逆时针旋转90°到△ADE的位置，求四边形ABCD的面积问题转化为求梯形ACDE的面积问题；根据全等三角形线段之间的关系，结合勾股定理，把梯形上底DE，下底AC，高DF分别用含x的式子表示，可表示四边形ABCD的面积．

作AE⊥AC，DE⊥AE，两线交于E点，作DF⊥AC垂足为F点，

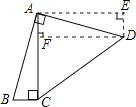
∵∠BAD=∠CAE=90°，即∠BAC+∠CAD=∠CAD+∠DAE

∴∠BAC=∠DAE

又∵AB=AD，∠ACB=∠E=90°

∴△ABC≌△ADE（AAS）

∴BC=DE，AC=AE，

设BC=a，则DE=a，DF=AE=AC=4BC=4a，

CF=AC-AF=AC-DE=3a，

在Rt△CDF中，由勾股定理得，

CF2+DF2=CD2，即（3a）2+（4a）2=x2，

解得：a=，

∴y=S四边形ABCD=S梯形ACDE=×（DE+AC）×DF

=×（a+4a）×4a

=10a2

=x2．

故选C．