题目内容
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
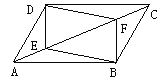
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.

求证CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴ ( ),
∵ DE∥BC(已证),
∴ ( ),
又∵∠1=∠2(已知),
∴ ( ),
∴CD∥FG( ),
∴ (两直线平行同位角相等),
∵ FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
即∠CDB=∠FGB=90°,
∴CD⊥AB. (垂直的定义).
【答案】见解析.
【解析】已知∠ADE=∠B,根据同位角相等,两直线平行可得DE∥BC,再由两直线平行,内错角相等可得∠1=∠DCF;又因∠1=∠2,根据等量代换可得∠DCF =∠2,根据同位角相等两直线平行得CD∥FG,再由两直线平行同位角相等得∠BDC =∠BGF,已知FG⊥AB,由垂直的定义可得∠FGB=90°,即可得∠CDB=∠FGB=90°,所以CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴ DE∥BC ( 同位角相等,两直线平行 ),
∵ DE∥BC(已证),
∴ ∠1=∠DCF ( 两直线平行,内错角相等 ),
又∵∠1=∠2(已知),
∴ ∠DCF =∠2 (等量代换 ),
∴CD∥FG( 同位角相等,两直线平行),
∴ ∠BDC =∠BGF (两直线平行,同位角相等),
∵ FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
即∠CDB=∠FGB=90°,
∴CD⊥AB. (垂直的定义).

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】如图是生活中常见的月历的示意图,请结合图示回答下列问题.
一 | 二 | 三 | 四 | 五 | 六 | 日 |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)如图是另一个月的月历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d分别与a的关系:b=________;c=________;d=________(用含a的代数式填空).
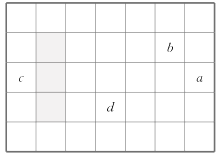
(2)用一个长方形框圈出月历中的三个数(如 图中的阴影),若这三个数之和等于51,则这三个数分别是多少?
(3)这样圈出的三个数的和可能是64吗?为什么?