Question

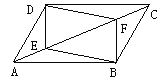
【题目】如图，□ABCD中，点E、F在对角线AC上，且AE=CF。求证：四边形BEDF是平行四边形。

Answer 1

【答案】证明见解析

【解析】试题分析：

由题意知，AC为平行四边形ABCD的对角线，条件中的AE与CF又是对角线AC的一部分，容易联想到利用平行四边形对角线的相关性质解决该题. 为了利用对角线的性质，可以作出对角线BD，进而容易看出四边形BEDF的两条对角线互相平分，利用平行四边形的相应判定定理即可得证.

试题解析：

连接BD交AC于点O. (如图)

∵四边形ABCD是平行四边形，

∴OA=OC，OB=OD，

又∵AE=CF，

∴OA-AE=OC-CF，

即OE=OF，

∵在四边形BEDF中，OE=OF，OB=OD，

∴四边形BEDF为平行四边形.