��Ŀ����
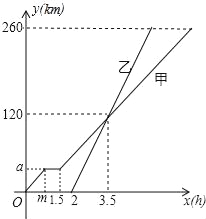
����Ŀ����ͼ��һС���б��O�㴦�׳�������׳�·�߿����ö��κ���y=��x2+4x�̻���б�¿�����һ�κ���y= ![]() x�̻���
x�̻���
��1�������䷽������κ���ͼ�����ߵ�P�����ꣻ
��2��С��������A�����A�����ꣻ
��3�����������ߵ���ߵ�P���O��A�á�POA�����POA�������
��4����OA�Ϸ����������ϴ���һ��M��M��P���غϣ�����MOA��������ڡ�POA���������ֱ��д����M�����꣮
���𰸡�
��1���⣺������ã�y=��x2+4x=����x��2��2+4��
�ʶ��κ���ͼ�����ߵ�P������Ϊ��2��4��
��2���⣺����������ʽ�ɵã� 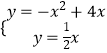 ��
��
��ã� ![]() ����
���� ![]() ��
��
�ʿɵõ�A������Ϊ�� ![]() ��
�� ![]() ��
��
��3���⣺��ͼ����PQ��x���ڵ�Q��AB��x���ڵ�B��
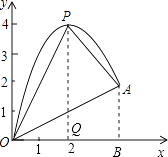
S��POA=S��POQ+S����PQBA��S��BOA
= ![]() ��2��4+
��2��4+ ![]() ����
���� ![]() +4������
+4������ ![]() ��2����
��2���� ![]() ��
�� ![]() ��
�� ![]()
=4+ ![]() ��
�� ![]()
= ![]()
��4���⣺��P��OA��ƽ���ߣ����������ڵ�M������OM��AM�����MOA��������ڡ�POA�������
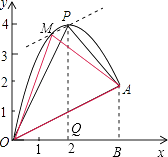
��ֱ��PM�Ľ���ʽΪy= ![]() x+b��
x+b��
��P��������2��4����
��4= ![]() ��2+b�����b=3��
��2+b�����b=3��
��ֱ��PM�Ľ���ʽΪy= ![]() x+3��
x+3��
�� 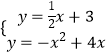 �����
����� ![]() ��
�� 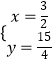 ��
��
���M�������� ![]() ��
�� ![]() ����
����
����������1�������䷽������ɶ���ʽ����2��A��������ͨ������������ֱ�߽���ʽ�����ķ�����Ľ⼴�ɣ���3����б�����Ρ������ͨ��������ת��Ϊ����ֱ�����Ρ�������ͣ���4���ױ߹��õ������������ȿ�����˼ά�����ɡ�ƽ�������еĵױ߹��������������ȡ��õ�ֱ��PM![]() OA�����PM����ʽ�������ߵĽ��㣬�������M����.
OA�����PM����ʽ�������ߵĽ��㣬�������M����.

����Ŀ����֪��A1B1C1���ɡ�ABC����ƽ�Ƶõ��ģ����У�A��B��C����Ķ�Ӧ��ֱ���A1��B1��C1��������ƽ��ֱ������ϵ�е��������±���ʾ��
��ABC | A��a��0�� | B��3��0�� | C��5��5�� |
��A1B1C1 | A1����3��2�� | B1����1��b�� | C1��c��7�� |
��1���۲���и���Ӧ������ı仯������գ�a=�� ����b=�� ����c=�� ����
��2������ͼ��ƽ��ֱ������ϵ�л�����ABC����A1B1C1��
��3����A1B1C1��������� ����