题目内容
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边。
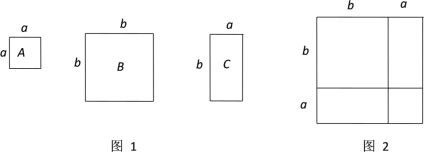
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称;
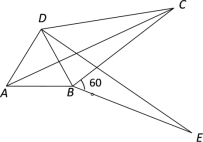
(2)如图,将![]() 绕顶点B顺时针方向旋转
绕顶点B顺时针方向旋转![]() ,得到
,得到![]() ,连接AD、DC,
,连接AD、DC,![]() ,求证:
,求证:![]() ,即四边形ABCD是勾股四边形。
,即四边形ABCD是勾股四边形。
【答案】(1)正方形、长方形、直角梯形(任选两个均可);(2)证明过程见解析.
【解析】
(1)只要四边形中有一个角是直角,根据勾股定理就有两直角边平方的和等于斜边的平方,即此四边形中存在相邻两边的平方和等于一条对角线的平方,由此可知,正方形、长方形、直角梯形都是勾股四边形.
(2)首先证明△ABC≌△DBE,得出AC=DE,BC=BE,连接CE,进一步得出△BCE为等边三角形;利用等边三角形的性质,进一步得出△DCE是直角三角形,问题得解.
解:(1)正方形、长方形、直角梯形(任选两个均可)
(2)证明:连结EC
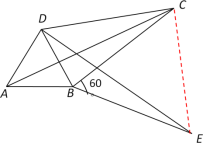
∵△DBE是由△ABC绕顶点B顺时针方向旋转![]() 得到
得到
∴△ABC≌△DBE,
∴AC=DE,BC=BE,
∵![]() ∠CBE=60°,
∠CBE=60°,
∴EC=BC=BE,∠BCE=60°,
∵∠DCB=30°,
∴△DCE=90°,
∴DC2+CE2=DE2,
∴DC2+BC2=AC2,
即四边形ABCD是勾股四边形.
故答案为:(1)正方形、长方形、直角梯形(任选两个均可);(2)证明过程见解析.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?