题目内容
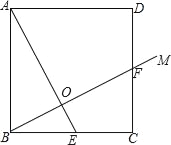
【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
①E为AB的中点;
②FC=4DF;
③S△ECF= ![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 . 
【答案】①③④
【解析】解:∵M、N是BD的三等分点,
∴DN=NM=BM,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△BEM∽△CDM,
∴ ![]() ,
,
∴BE= ![]() CD,
CD,
∴BE= ![]() AB,故①正确;
AB,故①正确;
∵AB∥CD,
∴△DFN∽△BEN,
∴ ![]() =
= ![]() ,
,
∴DF= ![]() BE,
BE,
∴DF= ![]() AB=
AB= ![]() CD,
CD,
∴CF=3DF,故②错误;
∵BM=MN,CM=2EM,
∴S△BEM=S△EMN= ![]() S△CBE,
S△CBE,
∵BE= ![]() CD,CF=
CD,CF= ![]() CD,
CD,
∴ ![]() =
= ![]() ,
,
∴S△EFC= ![]() S△CBE=
S△CBE= ![]() S△MNE,
S△MNE,
∴S△ECF= ![]() ,故③正确;
,故③正确;
∵BM=NM,EM⊥BD,
∴EB=EN,
∴∠ENB=∠EBN,
∵CD∥AB,
∴∠ABN=∠CDB,
∵∠DNF=∠BNE,
∴∠CDN=∠DNF,
∴△DFN是等腰三角形,故④正确;
所以答案是:①③④.
【考点精析】掌握平行四边形的性质和相似三角形的判定与性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目