题目内容
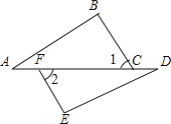
【题目】如图，在正方形ABCD（四个边相等，四个角为直角）中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP+EP最小值的是( )
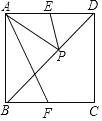
A. AB B. DE C. AF D. BD
【答案】C
【解析】
连接CP，当点E，P，C在同一直线上时，AP＋PE的最小值为CE长，依据△ABF≌△CDE，即可得到AP＋EP最小值等于线段AF的长．
如图，连接CP，
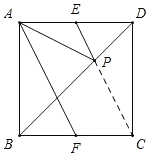
由AD＝CD，∠ADP＝∠CDP＝45°，DP＝DP，可得△ADP≌△CDP，
∴AP＝CP，
∴AP＋PE＝CP＋PE，
∴当点E，P，C在同一直线上时，AP＋PE的最小值为CE长，
此时，由AB＝CD，∠ABF＝∠CDE，BF＝DE，可得△ABF≌△CDE，
∴AF＝CE，
∴AP＋EP最小值等于线段AF的长，
故选：C．
练习册系列答案
口算能手系列答案
相关题目
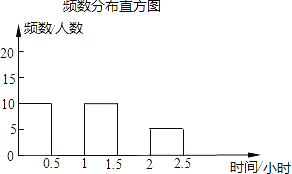
【题目】（根据市教委提出的学生每天体育锻炼不少于1小时的要求，为确保阳光体育运动时间得到落实，某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查，其中部分结果记录如下：
时间分组（小时） | 频数（人数） | 频率 |
0≤t＜0.5 | 10 | 0.2 |
0.5≤t＜1 | 0.4 | |
1≤t＜1.5 | 10 | 0.2 |
1.5≤t＜2 | 0.1 | |
2≤t＜2.5 | 5 | |
合计 | 1 |
请你将频数分布表和频数分布直方图补充完整．
