题目内容
【题目】在平行四边形 ABCD 中,AE 平分∠BAD 交边 BC 于 E,DF 平分∠ADC 交边 BC 于 F,若 AD=11,EF=5,则 AB= ___.
【答案】8或3
【解析】
根据AE和DF是否相交分类讨论,分别画出对应的图形,根据平行四边形的性质、平行线的性质、角平分线的定义和等角对等边即可得出结论.
解:①当AE和DF相交时,如下图所示
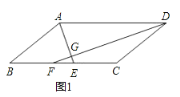
∵四边形ABCD为平行四边形,AD=11,EF=5,
∴BC=AD=11,AD∥BC,AB=CD
∴∠DAE=∠BEA,∠ADF=∠CFD
∵AE 平分∠BAD,DF 平分∠ADC
∴∠DAE=∠BAE,∠ADF=∠CDF
∴∠BEA=∠BAE,∠CFD=∠CDF
∴BE=AB,CF=CD
∴BE=AB= CD= CF
∵BE+CF=BC+EF
∴2AB=11+5
解得:AB=8;
②当AE和DF不相交时,如下图所示
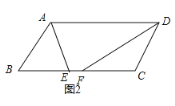
∵四边形ABCD为平行四边形,AD=11,EF=5,
∴BC=AD=11,AD∥BC,AB=CD
∴∠DAE=∠BEA,∠ADF=∠CFD
∵AE 平分∠BAD,DF 平分∠ADC
∴∠DAE=∠BAE,∠ADF=∠CDF
∴∠BEA=∠BAE,∠CFD=∠CDF
∴BE=AB,CF=CD
∴BE=AB= CD= CF
∵BE+CF+EF =BC
∴2AB+5=11
解得:AB=3
综上所述:AB=8或3
故答案为:8或3.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
【题目】为支援四川雅安地震灾区,某市民政局组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
甲种货车 | 乙种货车 | |
载货量(吨/辆) | 45 | 30 |
租金(元/辆) | 400 | 300 |
如果计划租用6辆货车,且租车的总费用不超过2300元,求最省钱的租车方案.