题目内容
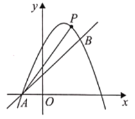
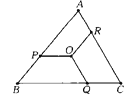
【题目】如图,点O在△ABC内,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR=x,BC=a,CA=b,AB=c,则x=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
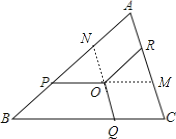
延长PO交AC于M,延长QO交AB于N,如图,设OP=OQ=OR=x,易证得四边形ANOR、四边形CMOQ为平行四边形,则MC=OQ=x,ON=AR,根据相似三角形的判定易得△ROM∽△ABC,利用相似比可得RM=![]() x,再判断△NOP∽△ACB,利用相似比可得NO=
x,再判断△NOP∽△ACB,利用相似比可得NO=![]() x,则AR=
x,则AR=![]() x,所以
x,所以![]() x+
x+![]() x+x=b,于是解得x=
x+x=b,于是解得x=![]() =
=![]() .
.
延长PO交AC于M,延长QO交AB于N,如图,
设OP=OQ=OR=x,
∵OP∥BC,OQ∥CA,OR∥AB,
∴四边形ANOR、四边形CMOQ为平行四边形,
∴MC=OQ=x,ON=AR,
易证得△ROM∽△ABC,
∴![]() ,即
,即![]() ,
,
∴RM=![]() x,
x,
易证得△NOP∽△ACB,
∴![]() ,即
,即![]() ,
,
∴NO=![]() x,
x,
∴AR=![]() x,
x,
∵AR+RM+MC=AC,
即![]() x+
x+![]() x+x=b,
x+x=b,
∴x=![]() =
=![]() ,
,
即OP的长为![]() .
.
故选A.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】某度假村拥有客房40间,该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系:
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式.
(2)已知租出的每间客房每日需要清洁费80元,未租出的每间客房每日需要清洁费40元.含x(x≥200)的代数式填表:
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板,你会将每间客房的日租金定为多少元,才能使度假村获得最大日收益?最大日收益是多少元?