题目内容
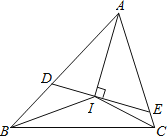
【题目】我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.

(1)请你通过画图、度量,填写右上表(图画在草稿纸上,并尽量画准确)
(2)从上表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理.

【答案】(1)∠BIC的度数110°;120°;135°;150°;∠BDI的度数110°;120°;135°;150°;(2)∠BIC=∠BDI
【解析】
试题分析:(1)通过画图、度量,即可完成表格;
(2)先从上表中发现∠BIC=∠BDI,再分别证明∠BIC=90°+![]() ∠BAC,∠BDI=90°+
∠BAC,∠BDI=90°+![]() ∠BAC.
∠BAC.
解:(1)填写表格如下:
∠BIC的度数110°;120°;135°;150°
∠BDI的度数110°;120°;135°;150°
(2)∠BIC=∠BDI,理由如下:
∵△ABC的三条内角平分线相交于点I,
∴∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣![]() (180°﹣∠BAC)
(180°﹣∠BAC)
=90+![]() ∠BAC;
∠BAC;
∵AI平分∠BAC,
∴∠DAI=![]() ∠DAE.
∠DAE.
∵DE⊥AI于I,
∴∠AID=90°.
∴∠BDI=∠AID+∠DAI=90°+![]() ∠BAC.
∠BAC.
∴∠BIC=∠BDI.

练习册系列答案
相关题目