题目内容
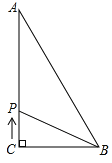
【题目】如图,△ABC中,∠C=900,AC=8cm,BC=6cm,,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分?
(2)当t为何值时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为12?
【答案】(1)6;(2)6.5;(3)2或6.5
【解析】
试题分析:(1)先求出△ABC的周长为24cm,所以当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,再根据时间=路程÷速度即可求解;
(2)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,进而求解即可;
(3)分两种情况:①P在AC上;②P在AB上.
试题解析:(1)△ABC中,∵AC=8cm,BC=6cm,AB=10cm,
∴△ABC的周长=8+6+10=24cm,
∴当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,
∴2t=12,t=6;
(2)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),
∴2t=13,t=6.5;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=12,
∴![]() ×6×CP=12,
×6×CP=12,
∴CP=4,
∴2t=4,t=2;
②当P在AB上时,
∵△BCP的面积=12=△ABC面积的一半,
∴P为AB中点,
∴2t=13,t=6.5.

【题目】根据下列表格的对应值,判断ax2+bx+c=0 (a≠0,a,b,c为常数)的一个解x的取值范围是_____
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |

