Question

【题目】定义：至少有一组对边相等的四边形为“等对边四边形”．

（1）请写出一个你学过的特殊四边形中是“等对边四边形”的名称；

（2）如图1，四边形ABCD是“等对边四边形”，其中AB=CD，边BA与CD的延长线交于点M，点E、F是对角线AC、BD的中点，若∠M=60°，求证：EFAB；

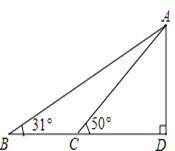
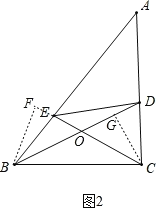
（3）如图2．在△ABC中，点D、E分别在边AC、AB上，且满足∠DBC=∠ECB∠A，线段CE、BD交于点．

①求证：∠BDC=∠AEC；

②请在图中找到一个“等对边四边形”，并给出证明．

Answer 1

【答案】（1）如：平行四边形、矩形、菱形、等腰梯形等；（2）证明见解析；（3）①证明见解析；②四边形EBCD是等对边四边形．证明见解析．

【解析】

（1）理解等对边四边形的图形的定义，有平行四边形、矩形、菱形、等腰梯形等，可得出答案．

（2）取BC的中点N，连结EN，FN，由中位线定理可得EN＝12CD，FN＝12AB，可证明△EFN为等边三角形，则结论得证；

（3）①证明∠EOB＝∠A，利用四边形内角和可证明∠BDC＝∠AEC；

②作CG⊥BD于G点，作BF⊥CE交CE延长线于F点．根据AAS可证明△BCF≌△CBG，则BF＝CG，证明△BEF≌△CDG，可得BE＝CD，则四边形EBCD是“等对边四边形”．

（1）如：平行四边形、矩形、菱形、等腰梯形等．

（2）如图1，取BC的中点N，连结EN，FN，

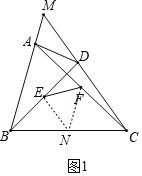
∴ENCD，FNAB，

∴EN=FN．

∵∠M=60°，

∴∠MBC+∠MCB=120°．

∵FN∥AB，EN∥MC，

∴∠FNC=∠MBC，∠ENB=∠MCB，

∴∠ENF=180°﹣120°=60°，

∴△EFN为等边三角形，

∴EF=FNAB．

（3）①证明：∵∠BOE=∠BCE+∠DBC，∠DBC=∠ECB∠A，

∴∠BOE=2∠DBC=∠A．

∵∠A+∠AEC+∠ADB+∠EOD=360°，∠BOE+∠EOD=180°，

∴∠AEC+∠ADB=180°．

∵∠ADB+∠BDC=180°，

∴∠BDC=∠AEC；

②解：此时存在等对边四边形，是四边形EBCD．

如图2，作CG⊥BD于G点，作BF⊥CE交CE延长线于F点．

∵∠DBC=∠ECB∠A，BC=CB，∠BFC=∠BGC=90°，

∴△BCF≌△CBG(AAS)，

∴BF=CG．

∵∠BEF=∠ABD+∠DBC+∠ECB，∠BDC=∠ABD+∠A，

∴∠BEF=∠BDC，

∴△BEF≌△CDG(AAS)，

∴BE=CD，

∴四边形EBCD是等对边四边形．