Question

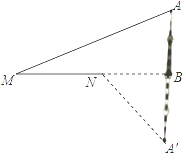
【题目】如图，在△ABC和△ADE中，AB=AD，AC=AE，∠1=∠2

（1）求证：△ABC≌△ADE；

（2）找出图中与∠1、∠2相等的角（直接写出结论，不需证明）．

Answer 1

【答案】（1）证明见解析;（2）∠MFD和∠NFC,理由见解析.

【解析】

（1）根据等式性质可以得出∠BAC=∠DAE，进而运用SAS判定△ABC≌△ADE； （2）根据全等三角形的对应角相等，可以发现∠B=∠D，∠E=∠C，进而得出与∠1、∠2相等的角有∠MFD和∠NFC．

本题解析：

（1）证明：∵∠1=∠2，

∴∠1+∠MAC=∠2+∠NAC，

∴∠BAC=∠DAE，

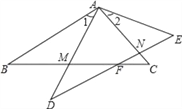
在△ABC和△ADE中，

，

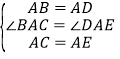∴△ABC≌△ADE（SAS）；

（2）图中与∠1、∠2相等的角有∠MFD和∠NFC．