题目内容
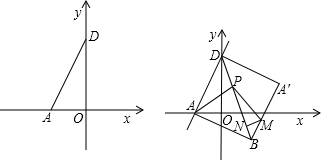
如图,在直角坐标系中,A的坐标为(a,0),D的坐标为(0,b),且a、b满足
+(b-4)2=0
(1)求A、D两点的坐标;
(2)以A为直角顶点作等腰直角三角形△ADB,直接写出B的坐标;
(3)在(2)的条件下,当点B在第四象限时,将△ADB沿直线BD翻折得到△A′DB,点P为线段BD上一动点(不与B、D重合),PM⊥PA交A′B于M,且PM=PA,MN⊥PB于N,请探究:PD、PN、BN之间的数量关系.
| a+2 |
(1)求A、D两点的坐标;
(2)以A为直角顶点作等腰直角三角形△ADB,直接写出B的坐标;
(3)在(2)的条件下,当点B在第四象限时,将△ADB沿直线BD翻折得到△A′DB,点P为线段BD上一动点(不与B、D重合),PM⊥PA交A′B于M,且PM=PA,MN⊥PB于N,请探究:PD、PN、BN之间的数量关系.

分析:(1)由非负数的性质,即可求得a与b的值,继而求得A、D两点的坐标;
(2)由等腰直角三角形的性质,可证得△ACB1≌△DOA,继而求得答案;
(3)首先过点A作AE⊥BD于点E,易证得四边形ABA′D是正方形,△APE≌△PMN,继而证得PN=PD+BN.
(2)由等腰直角三角形的性质,可证得△ACB1≌△DOA,继而求得答案;
(3)首先过点A作AE⊥BD于点E,易证得四边形ABA′D是正方形,△APE≌△PMN,继而证得PN=PD+BN.
解答:解:(1)∵a、b满足
+(b-4)2=0,
∴a+2=0,b-4=0,
解得:a=-2,b=4,
∴A、D两点的坐标分别为:(-2,0),(0,4);
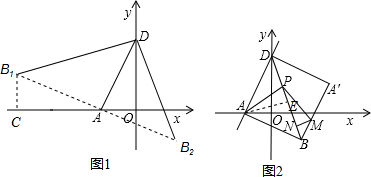
(2)如图1,过点B1作B1C⊥x轴于点C,
∵△AB1D是等腰直角三角形,
∴AB1=AD,∠B1AC+∠OAD=90°,
∵∠OAD+∠ADO=90°,
∴∠B1AC=∠ADO,
 ∵在△ACB1和△DOA中,
∵在△ACB1和△DOA中,
,
∴△ACB1≌△DOA(AAS),
∴AC=OD=4,B1C=OA=2,
∴OC=OA+AC=6,
∴点B1的坐标为:(-6,2);
同理:点B2的坐标为:(4,-2);
综上:点B的坐标为:(-6,2),(4,-2);
(3)PN=PD+BN.
如图2,过点A作AE⊥BD于点E,
由折叠的性质可得:AD=A′D,AB=A′B,
∵AD=AB,
∴AD=AB=A′D=A′B,
∴四边形ABA′D是菱形,
∵∠DAB=90°,
∴菱形ABA′D是正方形,
∴DE=BE=
BD,∠A′BN=45°,
∵MN⊥BD,
∴△BMN是等腰直角三角形,
∴MN=BN,
∵PM⊥PA,
∴∠APE+∠MPN=90°,
∵∠APE+∠PAE=90°,
∴∠PAE=∠MPN,
∵在△APE和△PMN中,
,
∴△APE≌△PMN(AAS),
∴PE=MN,
∴PE=BN,
∴PN=PE+EN=BN+EN=BE,PD+PE=PD+BN=DE,
∴PN=PD+BN.
| a+2 |
∴a+2=0,b-4=0,
解得:a=-2,b=4,
∴A、D两点的坐标分别为:(-2,0),(0,4);
(2)如图1,过点B1作B1C⊥x轴于点C,
∵△AB1D是等腰直角三角形,
∴AB1=AD,∠B1AC+∠OAD=90°,
∵∠OAD+∠ADO=90°,
∴∠B1AC=∠ADO,
 ∵在△ACB1和△DOA中,
∵在△ACB1和△DOA中,
|
∴△ACB1≌△DOA(AAS),
∴AC=OD=4,B1C=OA=2,
∴OC=OA+AC=6,
∴点B1的坐标为:(-6,2);
同理:点B2的坐标为:(4,-2);
综上:点B的坐标为:(-6,2),(4,-2);
(3)PN=PD+BN.
如图2,过点A作AE⊥BD于点E,
由折叠的性质可得:AD=A′D,AB=A′B,
∵AD=AB,
∴AD=AB=A′D=A′B,
∴四边形ABA′D是菱形,
∵∠DAB=90°,
∴菱形ABA′D是正方形,
∴DE=BE=
| 1 |
| 2 |
∵MN⊥BD,
∴△BMN是等腰直角三角形,
∴MN=BN,
∵PM⊥PA,
∴∠APE+∠MPN=90°,
∵∠APE+∠PAE=90°,
∴∠PAE=∠MPN,
∵在△APE和△PMN中,
|
∴△APE≌△PMN(AAS),
∴PE=MN,
∴PE=BN,
∴PN=PE+EN=BN+EN=BE,PD+PE=PD+BN=DE,
∴PN=PD+BN.
点评:此题考查了折叠的性质、正方形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质以及非负数的性质等知识.此题综合性较强,难度较大,注意掌握折叠前后图形的对应关系,注意辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

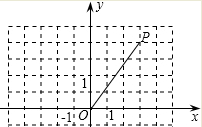 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
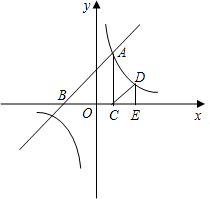
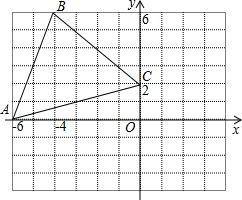 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: