题目内容
如图,在直角坐标系中,⊙M与y轴相切于点C,与x轴交于A(x1,0),B(x2,0)两点,其中x1,x2 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
(1)求过A、B、C三点的抛物线的解析式;
(2)判断直线NA与⊙M的位置关系,并说明理由;
(3)一动点P从点C出发,以每秒1个单位长的速度沿CM向点M运动,同时,一动点Q从点B出发,沿射线BA以每秒4个单位长度的速度运动,当P运动到M点时,两动点同时停止运动,当时间t为何值时,以Q、O、C为顶点的三角形与△PCO相似?
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.(1)求过A、B、C三点的抛物线的解析式;
(2)判断直线NA与⊙M的位置关系,并说明理由;
(3)一动点P从点C出发,以每秒1个单位长的速度沿CM向点M运动,同时,一动点Q从点B出发,沿射线BA以每秒4个单位长度的速度运动,当P运动到M点时,两动点同时停止运动,当时间t为何值时,以Q、O、C为顶点的三角形与△PCO相似?
分析:(1)先解方程x2-10x+16=0求出两根,确定A、B两点的坐标,再连接AM,过点M作MD⊥AB于D,由垂径定理得AD=
AB=3,D点的坐标为(5,0),则⊙M的半径为5,然后在直角△AMD中,运用勾股定理求出MD的长,得到点C的坐标,最后运用待定系数法即可求出过A、B、C三点的抛物线的解析式;
(2)先根据抛物线的解析式求出顶点N的坐标,再分别计算AN、MN,在△AMN中由勾股定理的逆定理可得∠MAN=90°,然后根据切线的判定定理即可判断直线NA与⊙M相切;
(3)由于0<t≤5,又t=2时,点Q运动到原点,此时以Q、O、C为顶点的三角形不存在,所以分两种情况讨论:①0<t<2,即点Q在x轴正半轴上;②2<t≤5,即点Q在x轴负半轴上.又因为以Q、O、C为顶点的三角形与△PCO都是直角三角形,则直角顶点O与C对应,每一种情况又分为两种:(Ⅰ)△QOC∽△PCO;(Ⅱ)△QOC∽△OCP.
| 1 |
| 2 |
(2)先根据抛物线的解析式求出顶点N的坐标,再分别计算AN、MN,在△AMN中由勾股定理的逆定理可得∠MAN=90°,然后根据切线的判定定理即可判断直线NA与⊙M相切;
(3)由于0<t≤5,又t=2时,点Q运动到原点,此时以Q、O、C为顶点的三角形不存在,所以分两种情况讨论:①0<t<2,即点Q在x轴正半轴上;②2<t≤5,即点Q在x轴负半轴上.又因为以Q、O、C为顶点的三角形与△PCO都是直角三角形,则直角顶点O与C对应,每一种情况又分为两种:(Ⅰ)△QOC∽△PCO;(Ⅱ)△QOC∽△OCP.
解答: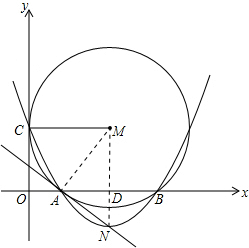 解:(1)解方程x2-10x+16=0,得x1=2,x2=8,
解:(1)解方程x2-10x+16=0,得x1=2,x2=8,
∴A(2,0),B(8,0).
连接AM,过点M作MD⊥AB于D,由垂径定理得AD=
AB=3,
∴OD=OA+AD=2+3=5,
∴D点的坐标为(5,0).
∵⊙M与y轴相切于点C,
∴⊙M的半径AM=CM=OD=5.
在直角△AMD中,∵∠ADM=90°,
∴MD=
=4,
∴点C的坐标为(0,4),点M的坐标为(5,4).
设过A、B、C三点的抛物线的解析式为y=a(x-2)(x-8),
将点C的坐标(0,4)代入,得4=16a,
解得a=
,
∴y=
(x-2)(x-8)=
x2-
x+4.
故所求抛物线的解析式为y=
x2-
x+4;
(2)直线NA与⊙M相切,理由如下:
连接MN.
∵y=
x2-
x+4=y=
(x2-10x)+4=
(x-5)2-
,
∴顶点N的坐标为(5,-
).
∵AN2=(5-2)2+(-
)2=9+
=
,
AM2=52=25,
MN2=(4+
)2=(
)2=
,
∴AN2+AM2=MN2,
∴∠MAN=90°,
又∵点A在⊙M上,
∴直线NA与⊙M相切;
(3)分两种情况:
①当0<t<2,即点Q在x轴正半轴上时,
CP=t,BQ=4t,OQ=OB-BQ=8-4t.
若△QOC∽△PCO,则OQ:CP=OC:CO,
∵OC=CO,
∴OQ=CP,
∴8-4t=t,
解得t=
;
若△QOC∽△OCP,则OQ:CO=OC:CP,
即(8-4t):4=4:t,
整理t2-2t+4=0,
∵△=4-16<0,
∴原方程无解;
②当2<t≤5,即点Q在x轴负半轴上时,
CP=t,BQ=4t,OQ=BQ-OB=4t-8.
若△QOC∽△PCO,则OQ:CP=OC:CO,
∵OC=CO,∴OQ=CP,
∴4t-8=t,
解得t=
;
若△QOC∽△OCP,则OQ:CO=OC:CP,
即(4t-8):4=4:t,
整理t2-2t-4=0,
解得t=1±
(负值舍去).
综上可知,当t为
秒
秒或(1+
)秒时,以Q、O、C为顶点的三角形与△PCO相似.
 解:(1)解方程x2-10x+16=0,得x1=2,x2=8,
解:(1)解方程x2-10x+16=0,得x1=2,x2=8,∴A(2,0),B(8,0).
连接AM,过点M作MD⊥AB于D,由垂径定理得AD=
| 1 |
| 2 |
∴OD=OA+AD=2+3=5,
∴D点的坐标为(5,0).
∵⊙M与y轴相切于点C,
∴⊙M的半径AM=CM=OD=5.
在直角△AMD中,∵∠ADM=90°,
∴MD=
| AM2-AD2 |
∴点C的坐标为(0,4),点M的坐标为(5,4).
设过A、B、C三点的抛物线的解析式为y=a(x-2)(x-8),
将点C的坐标(0,4)代入,得4=16a,
解得a=
| 1 |
| 4 |
∴y=
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 2 |
故所求抛物线的解析式为y=
| 1 |
| 4 |
| 5 |
| 2 |
(2)直线NA与⊙M相切,理由如下:
连接MN.
∵y=
| 1 |
| 4 |
| 5 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
∴顶点N的坐标为(5,-
| 9 |
| 4 |
∵AN2=(5-2)2+(-
| 9 |
| 4 |
| 81 |
| 16 |
| 225 |
| 16 |
AM2=52=25,
MN2=(4+
| 9 |
| 4 |
| 25 |
| 4 |
| 625 |
| 16 |
∴AN2+AM2=MN2,
∴∠MAN=90°,
又∵点A在⊙M上,
∴直线NA与⊙M相切;
(3)分两种情况:
①当0<t<2,即点Q在x轴正半轴上时,
CP=t,BQ=4t,OQ=OB-BQ=8-4t.
若△QOC∽△PCO,则OQ:CP=OC:CO,
∵OC=CO,
∴OQ=CP,
∴8-4t=t,
解得t=
| 8 |
| 5 |
若△QOC∽△OCP,则OQ:CO=OC:CP,
即(8-4t):4=4:t,
整理t2-2t+4=0,
∵△=4-16<0,
∴原方程无解;
②当2<t≤5,即点Q在x轴负半轴上时,
CP=t,BQ=4t,OQ=BQ-OB=4t-8.
若△QOC∽△PCO,则OQ:CP=OC:CO,
∵OC=CO,∴OQ=CP,
∴4t-8=t,
解得t=
| 8 |
| 3 |
若△QOC∽△OCP,则OQ:CO=OC:CP,
即(4t-8):4=4:t,
整理t2-2t-4=0,
解得t=1±
| 5 |
综上可知,当t为
| 8 |
| 5 |
| 8 |
| 3 |
| 5 |
点评:本题考查了二次函数的综合题型,其中涉及到的知识点有一元二次方程的解法,垂径定理,勾股定理及其逆定理,运用待定系数法求二次函数的解析式,切线的判定,相似三角形的判定.在求有关动点问题时要注意分情况讨论,这是解题的关键.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: