Question

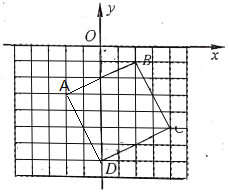
【题目】如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数的图象上，从左向右第3个正方形中的一个顶点A的坐标为，阴影三角形部分的面积从左向右依次记为、、、、，则的值为______用含n的代数式表示，n为正整数

Answer 1

【答案】

【解析】分析：

由题意可知Sn是第2n个正方形和第（2n-1）个正方形之间的阴影部分，先由已知条件分别求出图中第1个、第2个、第3个和第4个正方形的边长，并由此计算出S1、S2，并分析得到Sn与n间的关系，这样即可把Sn给表达出来了.

详解：

∵函数y=x与x轴的夹角为45°，
∴直线y=x与正方形的边围成的三角形是等腰直角三角形，
∵A（8，4），
∴第四个正方形的边长为8，
第三个正方形的边长为4，
第二个正方形的边长为2，
第一个正方形的边长为1，
…，
第n个正方形的边长为，第（n-1）个正方形的边长为，
由图可知，S1=，

S2=，

…，

由此可知Sn=第（2n-1）个正方形面积的一半，

∵第（2n-1）个正方形的边长为，

∴Sn=.
故答案为： .