题目内容
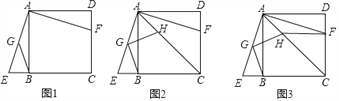
【题目】某数学活动小组在做角的拓展图形练习时,经历了如下过程:

(1)操作发现:点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,如图:将图1中的三角板绕点
的下方,如图:将图1中的三角板绕点![]() 旋转,当直角三角板的
旋转,当直角三角板的![]() 边在
边在![]() 的内部,且恰好平分
的内部,且恰好平分![]() 时,如图2.则下列结论正确的是 (填序号即可).
时,如图2.则下列结论正确的是 (填序号即可).
①![]() ②
②![]() ③
③![]() 平分
平分![]() ④
④![]() 的平分线在直线
的平分线在直线![]() 上
上
(2)数学思考:同学们在操作中发现,当三角板绕点![]() 旋转时,如果直角三角板的
旋转时,如果直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方,那么
在直线AB的下方,那么![]() 与
与![]() 的差不变,请你说明理由;如果直角三角板的
的差不变,请你说明理由;如果直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部,那么
的内部,那么![]() 与
与![]() 的和不变,请直接写出
的和不变,请直接写出![]() 与
与![]() 的和,不要求说明理由.
的和,不要求说明理由.
(3)类比探索:三角板绕点![]() 继续旋转,当直角三角板的
继续旋转,当直角三角板的![]() 边在
边在![]() 的内部时,如图3,求
的内部时,如图3,求![]() 与
与![]() 相差多少度?为什么?
相差多少度?为什么?
【答案】(1)①②④;(2)如果直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方,那么
在直线AB的下方,那么![]() 与
与![]() 的差不变,理由见解析;如果直角三角板的
的差不变,理由见解析;如果直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部,那么
的内部,那么![]() 与
与![]() 的和不变,
的和不变,![]() +
+![]() =30°;③30°.
=30°;③30°.
【解析】
(1)利用角平分线的定义结合直角三角板的内角度数即可分别判断得出答案;
(2)当直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方时根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,可得出结果;当直角三角板的
在直线AB的下方时根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,可得出结果;当直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部时,∠COM+∠BON=∠BOC-∠MON,可得出结果;
的内部时,∠COM+∠BON=∠BOC-∠MON,可得出结果;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,然后作差即可.
解:(1)∵![]() ,
,![]() 平分
平分![]() ,∴
,∴![]() ,故①正确;
,故①正确;
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,故②正确;
,故②正确;
∵![]() ,
,![]() ,∴
,∴![]() 不平分
不平分![]() ,故③错误;
,故③错误;
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() 的平分线在直线
的平分线在直线![]() 上,故④正确;
上,故④正确;
故答案为:①②④.
(2)![]() 与
与![]() 的差不变.理由如下:当直角三角板的
的差不变.理由如下:当直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方时,
在直线AB的下方时,
∵∠COM=∠BOC-∠COM=120°-∠BOM,
∠BON=∠MON-∠BOM=90°-∠BOM,
∴∠COM-∠BON=120°-90°=30°;![]() 与
与![]() 的和不变,其和为30°.理由如下:当直角三角板的
的和不变,其和为30°.理由如下:当直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部时,∠COM+∠BON=∠BOC-∠MON=120°-90°=30°.
的内部时,∠COM+∠BON=∠BOC-∠MON=120°-90°=30°.
(3)∵![]() ,
,![]() ,
,
∴![]() .
.