Question

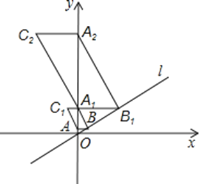
【题目】如图，在直角坐标系中，直线l与y轴正半轴所夹的锐角为60°，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1，以A1B、BA为邻边作□ABA1C1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2，以A2B1、B1A1为邻边作□A1B1A2C2；…；按此作法继续下去，则C3的坐标是 ____________；Cn的坐标是 _____________________

Answer 1

【答案】

【解析】

根据平行四边形的性质结合解直角三角形即可得出点C1、C2、C3的坐标，由此即可找出变化规律“点Cn的坐标是（-22（n-1），22n）（n为正整数）”，此题得解．

∵∠AOB=60°，OA=1，

∴AB=OAtan∠AOB=，AA1=ABtan∠ABA1=3，

∴点C1的坐标是（-，4）．

同理可得出：点C2的坐标是（-4，16），点C3的坐标是（-16，64），

∴点Cn的坐标是（-22（n-1），22n）（n为正整数）．

故答案为：（-16，64）；（-22（n-1），22n）（n为正整数）．