题目内容
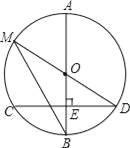
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
【答案】(1)13;(2)4![]() .
.
【解析】试题分析:(1)根据垂径定理求出DE的长,设出半径,根据勾股定理,列出方程求出半径;
(2)根据OM=OB,证出∠M=∠B,根据∠M=∠D,求出∠D的度数,根据锐角三角函数求出OE的长.
试题解析:(1)设⊙O的半径为x,则OE=x﹣8,
∵CD=24,由垂径定理得,DE=12,
在Rt△ODE中,OD2=DE2+OE2,
x2=(x﹣8)2+122,
解得:x=13.
(2)∵OM=OB,
∴∠M=∠B,
∴∠DOE=2∠M,
又∠M=∠D,
∴∠D=30°,
在Rt△OED中,∵DE=12,∠D=30°,
∴OE=4![]() .
.

练习册系列答案
相关题目