Question

【题目】如图1，在矩形ABCD中，AB＝4，BC＝3，以AB为直径的半圆O在矩形ABCD的外部，将半圆O绕点A顺时针旋转a度（0°≤a≤180°）．

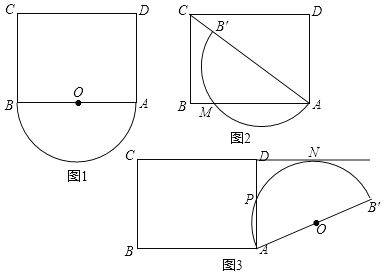
（1）在旋转过程中，B′C的最小值是　 　，如图2，当半圆O的直径落在对角线AC上时，设半圆O与AB的交点为M，则AM的长为　

（2）如图3，当半圆O与直线CD相切时，切点为N，与线段AD的交点为P，求劣弧AP的长；

（3）在旋转过程中，当半圆弧与直线CD只有一个交点时，设此交点与点C的距离为d，请直接写出d的取值范围．

Answer 1

【答案】（1）1，；（2）AP的长＝；（3）4﹣≤d＜4或d＝4+.

【解析】

（1）连接B′M，则∠B′MA＝90°，在Rt△ABC中，利用勾股定理可求出AC的长度，由∠B＝∠B′MA＝90°、∠BCA＝∠MAB′可得出△ABC∽△AMB′，根据相似三角形的性质可求出AM的长度；

（2）连接OP、ON，过点O作OG⊥AD于点G，则四边形DGON为矩形，进而可得出DG、AG的长度，在Rt△AGO中，由AO＝2、AG＝1可得出∠OAG＝60°，进而可得出△AOP为等边三角形，再利用弧长公式即可求出劣弧AP的长；

（3）由（2）可知：△AOP为等边三角形，根据等边三角形的性质可求出OG、DN的长度，进而可得出CN的长度，画出点B′在直线CD上的图形，在Rt△AB′D中（点B′在点D左边），利用勾股定理可求出B′D的长度进而可得出CB′的长度，再结合图形即可得出：半圆弧与直线CD只有一个交点时d的取值范围．

解：（1）∵在矩形ABCD中，AB＝4，BC＝3，

∴AC＝5，

在旋转过程中，当点B′落在对角线AC上时，B′C的值最小，最小值为1；

在图2中，连接B′M，则∠B′MA＝90°．

在Rt△ABC中，AB＝4，BC＝3，

∴AC＝5．

∵∠B＝∠B′MA＝90°，∠BCA＝∠MAB′，

∴△ABC∽△AMB′，

∴，即，

∴AM＝；

故答案为：1，；

（2）在图3中，连接OP、ON，过点O作OG⊥AD于点G．

∵半圆与直线CD相切，

∴ON⊥DN，

∴四边形DGON为矩形，

∴DG＝ON＝2，

∴AG＝AD﹣DG＝1．

在Rt△AGO中，∠AGO＝90°，AO＝2，AG＝1，

∴∠AOG＝30°，∠OAG＝60°．

又∵OA＝OP，

∴△AOP为等边三角形，

∴劣弧AP的长＝；

（3）由（2）可知：△AOP为等边三角形，

∴DN＝GO＝OA＝，

∴CN＝CD+DN＝4+，

当点B′在直线CD上时，如图4所示．

在Rt△AB′D中（点B′在点D左边），AB′＝4，AD＝3，

∴B′D＝，

∴CB′＝4﹣，

∵AB′为直径，

∴∠ADB′＝90°，

∴当点B′在点D右边时，半圆交直线CD于点D、B′．

∴当半圆弧与直线CD只有一个交点时，4﹣≤d＜4或d＝4+．