题目内容
【题目】我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”，三斜即指三角形的三条边长，可以用该方法求三角形面积．若改用现代数学语言表示，其形式为：设
为三角形三边，
为面积，则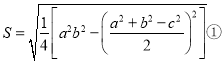
，这是中国古代数学的瑰宝之一．而在文明古国古希腊，也有一个数学家海伦给出了求三角形面积的另一个公式，若设
（周长的一半），则
（1）尝试验证．这两个公式在表面上形式很不一致，请你用以
为三边构成的三角形，分别验证它们的面积值；
（2）问题探究．经过验证，你发现公式①和②等价吗？若等价，请给出一个一般性推导过程（可以从
或者
）；
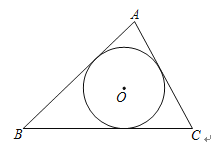
（3）问题引申．三角形的面积是数学中非常重要的一个几何度量值，很多数学家给出了不同形式的计算公式．请你证明如下这个公式：如图，
的内切圆半径为
，三角形三边长为，仍记，为三角形面积，则
．
【答案】（1）
；（2）公式
和
等价；推导过程见解析；（3）见解析．
【解析】
分别将5,7,8代入两个公式计算验证即可；
求出
，把①中根号内的式子可化为：
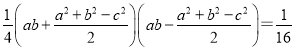
，即可得出结论；
连接
，
，由三角形面积公式即可得出结论．
解：由得：
，
由得：
，
；
公式和等价；推导过程如下：
，
，
中根号内的式子可化为：
，
；
连接，如图所示：
．
练习册系列答案
相关题目
