题目内容
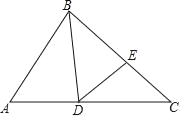
【题目】已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
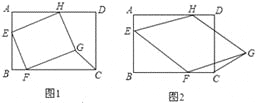
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
【答案】(1)10;(2)12-a;(3)不能
【解析】解:(1)过点G作GM⊥BC于M.在正方形EFGH中,
∠HEF=90°,EH=EF,
∴∠AEH+∠BEF=90°.
∵∠AEH+∠AHE=90°,
∴∠AHE=∠BEF.
又∵∠A=∠B=90°,
∴△AHE≌△BEF.
同理可证△MFG≌△BEF.
∴GM=BF=AE=2.∴FC=BC-BF=10.
∴![]() .
.
(2)过点G作GM⊥BC交BC的延长线于M,连接HF.
∵AD∥BC,∴∠AHF=∠MFH.
∵EH∥FG,∴∠EHF=∠GFH.
∴∠AHE=∠MFG.
又∵∠A=∠GMF=90°,EH=GF,
∴△AHE≌△MFG.∴GM=AE=2.
∴![]() .
.
(3)△GFC的面积不能等于2.
说明一:∵若S△GFC=2,则12-a=2,∴a=10.
此时,在△BEF中,
![]() .
.
在△AHE中,
![]() ,
,
∴AH>AD,即点H已经不在边AD上,故不可能有S△GFC=2.
说明二:△GFC的面积不能等于2.∵点H在AD上,
∴菱形边EH的最大值为![]() ,∴BF的最大值为
,∴BF的最大值为![]() .
.
又∵函数S△GFC=12-a的值随着a的增大而减小,
∴S△GFC的最小值为![]() .
.
又∵![]() ,∴△GFC的面积不能等于2.
,∴△GFC的面积不能等于2.

【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.