题目内容
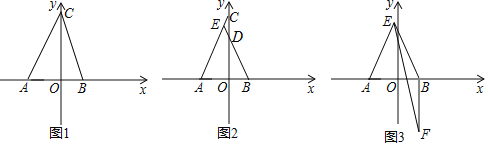
【题目】如图1,在△ABC中,点D为AB的中点,过点D作DE∥BC交AC于E.
(1)求证:E为AC的中点;
(2)如图2,过点D作QD⊥AB交BC的延长线于Q,过点E作EP⊥AC交CB的延长线于P,连AP、AQ.若PQ=12,AP+AQ=20,求DE的长.

【答案】(1)详见解析;(2)4
【解析】
(1)作CF∥AB交DE的延长线于点F,证明△ADE≌△CFE,根据全等三角形的性质得到AE=CE;
(2)根据线段垂直平分线的性质得到QA=QB,AP=CP,求出BC的长,根据三角形中位线定理解答即可.
(1)证明:作CF∥AB交DE的延长线于点F,
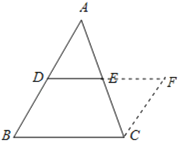
则∠A=∠FCE,
∵DE∥BC,CF∥AB,
∴四边形DBCF为平行四边形,
∴BD=CF,
∵点D为AB的中点,
∴AD=BD,
∴AD=CF,
在△ADE和△CFE中,
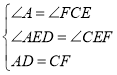 ,
,
∴△ADE≌△CFE(ASA),
∴AE=CE,即E为AC的中点;
(2)∵点D为AB的中点,QD⊥AB,
∴QA=QB,
同理,AP=CP,
∴BC=CP+BQ﹣PQ=AP+AQ﹣PQ=20﹣12=8,
∵D、E分别为AB、AC的中点,
∴DE=![]() BC=4
BC=4

练习册系列答案
相关题目