��Ŀ����
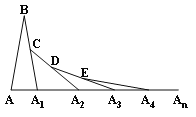
����Ŀ�������κ���y=ax2+bx+c��a��0����ͼ����x��Ľ�������ֱ�Ϊ��x1 �� 0������x2 �� 0������x1��x2 �� ͼ������һ��M��x0 �� y0����x���·�����������˵���� ��b2��4ac��0��
��x=x0�Ƿ���ax2+bx+c=y0�Ľ⣻
��x1��x0��x2
��a��x0��x1����x0��x2����0��
��x0��x1��x0��x2 ��
������ȷ���У� ��
A.�٢�
B.�٢ڢ�
C.�٢ڢ�
D.�٢ڢܢ�
���𰸡�B
���������⣺�١߶��κ���y=ax2+bx+c��a��0����ͼ����x��Ľ�������ֱ�Ϊ��x1 �� 0������x2 �� 0������x1��x2 �� ���ax2+bx+c=0����������ȵ�ʵ������
���=b2��4ac��0������ȷ���ڡ�ͼ������һ��M��x0 �� y0����
��a ![]() +bx0+c=y0 ��
+bx0+c=y0 ��
��x=x0�Ƿ���ax2+bx+c=y0�Ľ⣬����ȷ���۵�a��0ʱ����M��x0 �� y0����x���·���
��x1��x0��x2��
��a��0ʱ����M��x0 �� y0����x���·���
��x0��x1��x0��x2 �� �۴��ܡ߶��κ���y=ax2+bx+c��a��0����ͼ����x��Ľ�������ֱ�Ϊ��x1 �� 0������x2 �� 0����
��y=ax2+bx+c=a��x��x1����x��x2����
��ͼ������һ��M��x0 �� y0����x���·���
��y0=a��x0��x1����x0��x2����0������ȷ���ݸ��ݢۼ��ɵó��ݴ���
���Ͽ�֪��ȷ�Ľ����Т٢ڢܣ�
��ѡB��
�����㾫����������Ĺؼ�����������κ���ͼ���Լ�ϵ��a��b��c�Ĺ�ϵ�����֪ʶ�����ն��κ���y=ax2+bx+c�У�a��b��c�ĺ��壺a��ʾ���ڷ���a>0ʱ�������߿�������; a<0ʱ�������߿�������b��Գ����йأ��Գ���Ϊx=-b/2a;c��ʾ��������y��Ľ������꣺��0��c�����Լ�����������������Ľ�������⣬�˽�һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮

 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д�����Ŀ�������ڿ����еĴ����ٶ�v(m/s)���¶�T(��)�Ĺ�ϵ���±���
�¶�/�� | 0 | 5 | 10 | 15 | 20 |
�ٶ�v/(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)д���ٶ�v���¶�T֮��Ĺ�ϵʽ��
(2)��T��30��ʱ���������Ĵ����ٶȣ�
(3)�������Ĵ����ٶ�Ϊ346m/sʱ���¶��Ƕ��٣�